
Erdos–Ko–Rado theorem
Encyclopedia
In combinatorics
, the Erdős–Ko–Rado theorem of Paul Erdős
, Chao Ko
, and Richard Rado
is a theorem on hypergraph
s, specifically, on uniform hypergraphs of rank r.
The theorem is as follows. If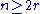 , and
, and 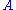 is a family of distinct subset
is a family of distinct subset
s of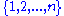 , such that each subset is of size
, such that each subset is of size  (thus making
(thus making 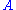 a uniform hypergraph of rank r), and each pair of subsets intersects
a uniform hypergraph of rank r), and each pair of subsets intersects
, then the maximum number of sets that can be in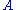 is given by the binomial coefficient
is given by the binomial coefficient
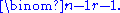
According to the theorem was proved in 1938, but was not published until 1961 in an apparently more general form. The subsets in question were only required to be size at most , and with the additional requirement that no subset be contained in any other. This statement is not actually more general: any subset that has size less than
, and with the additional requirement that no subset be contained in any other. This statement is not actually more general: any subset that has size less than  can be increased to size
can be increased to size  to make the above statement apply.
to make the above statement apply.
on n. In 1972, Gyula O. H. Katona
gave the following short proof using double counting
.
Suppose we have some such family of subsets A. Arrange the elements of {1, 2, ..., n} in any cyclic order, and consider the sets from A that form intervals of length r within this cyclic order. For example if n = 8 and r = 3, we could arrange the numbers {1, 2, ..., 8} into the cyclic order (3,1,5,4,2,7,6,8), which has eight intervals:, (1,5,4), (5,4,2), (4,2,7), (2,7,6), (7,6,8), (6,8,3), and (8,3,1).
However, it is not possible for all of the intervals of the cyclic order to belong to A, because some pairs of them are disjoint. Katona's key observation is that at most r of the intervals for a single cyclic order may belong to A. To see this, note that if (a1, a2, ..., ar) is one of these intervals in A, then every other interval of the same cyclic order that belongs to A separates ai and ai + 1 for some i (that is, it contains precisely one of these two elements). The two intervals that separate these elements are disjoint, so at most one of them can belong to A. Thus, the number of intervals in A is one plus the number of separated pairs, which is at most r.
Based on this idea, we may count the number of pairs (S,C), where S is a set in A and C is a cyclic order for which S is an interval, in two ways. First, for each set S one may generate C by choosing one of r! permutations of S and (n − r)! permutations of the remaining elements, showing that the number of pairs is |A|r!(n − r)!. And second, there are (n − 1)! cyclic orders, each of which has at most r intervals of A, so the number of pairs is at most r(n − 1)!. Combining these two counts gives the inequality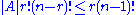
and dividing both sides by r!(n − r)! gives the result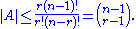
First, choose any fixed element x, and let A consist of all r-subsets of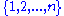 that include x. For instance, if n = 4, r = 2, and x = 1, this produces the family of three 2-sets
that include x. For instance, if n = 4, r = 2, and x = 1, this produces the family of three 2-sets
Any two sets in this family intersect, because they both include x.
Second, when n = 2r and with x as above, let A consist of all r-subsets of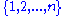 that do not include x.
that do not include x.
For the same parameters as above, this produces the family
Any two sets in this family have a total of 2r = n elements among them, chosen from the n − 1 elements that are unequal to x, so by the pigeonhole principle they must have an element in common.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the Erdős–Ko–Rado theorem of Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
, Chao Ko
Chao Ko
Ke Zhao or Chao Ko was a Chinese mathematician born in Wenling, Taizhou, Zhejiang, People's Republic of China.Zhao graduated from Tsinghua University in 1933 and obtained his doctorate from the University of Manchester under Louis Mordell in 1937. His main fields of study were algebra, number...
, and Richard Rado
Richard Rado
Richard Rado FRS was a Jewish German mathematician. He earned two Ph.D.s: in 1933 from the University of Berlin, and in 1935 from the University of Cambridge. He was interviewed in Berlin by Lord Cherwell for a scholarship given by the chemist Sir Robert Mond which provided financial support to...
is a theorem on hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s, specifically, on uniform hypergraphs of rank r.
The theorem is as follows. If
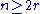 , and
, and 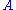 is a family of distinct subset
is a family of distinct subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of
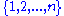 , such that each subset is of size
, such that each subset is of size  (thus making
(thus making 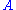 a uniform hypergraph of rank r), and each pair of subsets intersects
a uniform hypergraph of rank r), and each pair of subsets intersectsIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, then the maximum number of sets that can be in
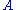 is given by the binomial coefficient
is given by the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
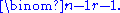
According to the theorem was proved in 1938, but was not published until 1961 in an apparently more general form. The subsets in question were only required to be size at most
 , and with the additional requirement that no subset be contained in any other. This statement is not actually more general: any subset that has size less than
, and with the additional requirement that no subset be contained in any other. This statement is not actually more general: any subset that has size less than  can be increased to size
can be increased to size  to make the above statement apply.
to make the above statement apply.Proof
The original proof of 1961 used inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
on n. In 1972, Gyula O. H. Katona
Gyula O. H. Katona
Gyula O. H. Katona is a Hungarian mathematician known for his work in combinatorial set theory, and especially for the Kruskal–Katona theorem and his elegant proof of the Erdős–Ko–Rado theorem...
gave the following short proof using double counting
Double counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
.
Suppose we have some such family of subsets A. Arrange the elements of {1, 2, ..., n} in any cyclic order, and consider the sets from A that form intervals of length r within this cyclic order. For example if n = 8 and r = 3, we could arrange the numbers {1, 2, ..., 8} into the cyclic order (3,1,5,4,2,7,6,8), which has eight intervals:, (1,5,4), (5,4,2), (4,2,7), (2,7,6), (7,6,8), (6,8,3), and (8,3,1).
However, it is not possible for all of the intervals of the cyclic order to belong to A, because some pairs of them are disjoint. Katona's key observation is that at most r of the intervals for a single cyclic order may belong to A. To see this, note that if (a1, a2, ..., ar) is one of these intervals in A, then every other interval of the same cyclic order that belongs to A separates ai and ai + 1 for some i (that is, it contains precisely one of these two elements). The two intervals that separate these elements are disjoint, so at most one of them can belong to A. Thus, the number of intervals in A is one plus the number of separated pairs, which is at most r.
Based on this idea, we may count the number of pairs (S,C), where S is a set in A and C is a cyclic order for which S is an interval, in two ways. First, for each set S one may generate C by choosing one of r! permutations of S and (n − r)! permutations of the remaining elements, showing that the number of pairs is |A|r!(n − r)!. And second, there are (n − 1)! cyclic orders, each of which has at most r intervals of A, so the number of pairs is at most r(n − 1)!. Combining these two counts gives the inequality
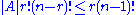
and dividing both sides by r!(n − r)! gives the result
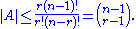
Families of maximum size
There are two different and straightforward constructions for a family of r-sets achieving the Erdős–Ko–Rado bound on cardinality.First, choose any fixed element x, and let A consist of all r-subsets of
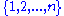 that include x. For instance, if n = 4, r = 2, and x = 1, this produces the family of three 2-sets
that include x. For instance, if n = 4, r = 2, and x = 1, this produces the family of three 2-sets
- {1,2}, {1,3}, {1,4}.
Any two sets in this family intersect, because they both include x.
Second, when n = 2r and with x as above, let A consist of all r-subsets of
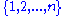 that do not include x.
that do not include x.For the same parameters as above, this produces the family
- {2,3}, {2,4}, {3,4}.
Any two sets in this family have a total of 2r = n elements among them, chosen from the n − 1 elements that are unequal to x, so by the pigeonhole principle they must have an element in common.

