In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, essential dimension is an invariant defined for certain algebraic structure

Algebraic structure

In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...

s such as algebraic group

Algebraic group

In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...

s and quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

s. It was introduced by J. Buhler and Z. Reichstein

Zinovy Reichstein

Zinovy Reichstein is a Russian-born American mathematician. He is a professor at the University of British Columbia in Vancouver.He studies mainly algebra, algebraic geometry and algebraic groups. He introduced the concept of essential dimension.Reichstein received his PhD degree in 1988 from...

 
and in its most generality defined by A. Merkurjev

Alexander Merkurjev

Alexander Merkurjev is a Russian-born American mathematician, who has made major contributions to the field of algebra. Currently Merkurjev is a professor at the University of California, Los Angeles.-Awards and distinctions:...

.
Basically, essential dimension measures the complexity of algebraic structures via their field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

s of definition. For example, a quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

 q : V → K over a field K, where V is a K-vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

, is said to be defined over a subfield L of K if there exists a K-basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

 e₁,...,e_n of V such that q can be expressed in the form 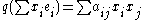with all coefficients a_ij belonging to L.