Alexander Merkurjev
Encyclopedia
Alexander Merkurjev is a Russia
n-born American mathematician, who has made major contributions to the field of algebra
. Currently Merkurjev is a professor at the University of California, Los Angeles
.
in Berkeley, California
, and his talk was entitled "Milnor K-theory and Galois cohomology". In 1995 he won the Humboldt Prize
, an international prize awarded to renowned scholars. Merkurjev gave a plenary talk at the 2nd European Congress of Mathematics
in Budapest, Hungary in 1996.
s, quadratic form
s, Galois cohomology
, algebraic K-theory
and central simple algebra
s. In the early 1980's Merkurjev proved a fundamental result about the structure of central simple algebras of period
dividing 2, which relates the 2-torsion of the Brauer group
with Milnor K-theory
. In subsequent work with Suslin
this was extended to higher torsion. More recently these results were generalized in the norm residue isomorphism theorem
(previously known as Bloch-Kato conjecture), proven in full generality by Rost
and Voevodsky
.
In the late 1990's Merkurjev gave the most general approach to the notion of essential dimension
, introduced by Buhler and Reichstein
, and made fundamental contributions to that field. In particular Merkurjev determined the essential p-dimension of central simple algebras of degree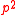
(for a prime p) and, in joint work with Karpenko, the essential dimension of finite p-groups.
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n-born American mathematician, who has made major contributions to the field of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. Currently Merkurjev is a professor at the University of California, Los Angeles
University of California, Los Angeles
The University of California, Los Angeles is a public research university located in the Westwood neighborhood of Los Angeles, California, USA. It was founded in 1919 as the "Southern Branch" of the University of California and is the second oldest of the ten campuses...
.
Awards and distinctions
In 1982 Merkurjev won the Young Mathematician Prize of the Petersburg Mathematical Society for his work on algebraic K-theory. In 1986 he was an invited speaker at the International Congress of MathematiciansInternational Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
in Berkeley, California
Berkeley, California
Berkeley is a city on the east shore of the San Francisco Bay in Northern California, United States. Its neighbors to the south are the cities of Oakland and Emeryville. To the north is the city of Albany and the unincorporated community of Kensington...
, and his talk was entitled "Milnor K-theory and Galois cohomology". In 1995 he won the Humboldt Prize
Humboldt Prize
The Humboldt Prize, also known as the Humboldt Research Award, is an award given by the Alexander von Humboldt Foundation to internationally renowned scientists and scholars, and is currently valued at € 60,000 with the possibility of further support during the prize winner's life. Up to one...
, an international prize awarded to renowned scholars. Merkurjev gave a plenary talk at the 2nd European Congress of Mathematics
European Congress of Mathematics
The European Congress of Mathematics is an international congress of the mathematics community, held every four years. Its objectives are "to present various new aspects of pure and applied mathematics to a wide audience, to be a forum for discussion of the relationship between mathematics and...
in Budapest, Hungary in 1996.
Work
Merkurjev's work focuses on algebraic groupAlgebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s, quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s, Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
, algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
and central simple algebra
Central simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
s. In the early 1980's Merkurjev proved a fundamental result about the structure of central simple algebras of period
Period
Period may mean a full stop: a punctuation in American-English.Period or periodic may also refer to:-Science:* Orbital period, a concept in astronomy...
dividing 2, which relates the 2-torsion of the Brauer group
Brauer group
In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
with Milnor K-theory
Milnor K-theory
In mathematics, Milnor K-theory was an early attempt to define higher algebraic K-theory, introduced by .The calculation of K2 of a field k led Milnor to the following ad hoc definition of "higher" K-groups by...
. In subsequent work with Suslin
Andrei Suslin
Andrei Suslin is a Russian mathematician who has made major contributions to the field of algebra, especially algebraic K-theory and its connections with algebraic geometry. He is currently a Trustee Chair and Professor of mathematics at Northwestern University.He was born on December 27, 1950,...
this was extended to higher torsion. More recently these results were generalized in the norm residue isomorphism theorem
Norm residue isomorphism theorem
In the mathematical field of algebraic K-theory, the norm residue isomorphism theorem is a long-sought result whose complete proof was announced in 2009...
(previously known as Bloch-Kato conjecture), proven in full generality by Rost
Markus Rost
Markus Rost is a German mathematician who works at the intersection of topology and algebra. He was an invited speaker at the International Congress of Mathematicians in 2002 in Beijing, China...
and Voevodsky
Vladimir Voevodsky
Vladimir Voevodsky is a Russian American mathematician. His work in developing a homotopy theory for algebraic varieties and formulating motivic cohomology led to the award of a Fields Medal in 2002.- Biography :...
.
In the late 1990's Merkurjev gave the most general approach to the notion of essential dimension
Essential dimension
In mathematics, essential dimension is an invariant defined for certain algebraic structures such as algebraic groups and quadratic forms. It was introduced by J. Buhler and Z. Reichstein and in its most generality defined by A. Merkurjev....
, introduced by Buhler and Reichstein
Zinovy Reichstein
Zinovy Reichstein is a Russian-born American mathematician. He is a professor at the University of British Columbia in Vancouver.He studies mainly algebra, algebraic geometry and algebraic groups. He introduced the concept of essential dimension.Reichstein received his PhD degree in 1988 from...
, and made fundamental contributions to that field. In particular Merkurjev determined the essential p-dimension of central simple algebras of degree
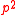(for a prime p) and, in joint work with Karpenko, the essential dimension of finite p-groups.