Estimation lemma
Encyclopedia
In mathematics, the estimation lemma gives an upper bound
for a contour integral. If f is a complex
-valued, continuous function
on the contour
and if its absolute value |f(z)| is bounded by a constant M for all z on 
, then
where
is the arc length
of
. In particular, we may take the maximum
as upper bound. Intuitively, the lemma
is very simple to understand. If a contour is thought of as many smaller contour segments connected together, then there will be a maximum |f(z)| for each segment. Out of all the maximum |f(z)|'s for the segments, there will be an overall largest one. Hence, if the overall largest |f(z)| is summed over the entire path then the integral of f(z) over the path must be less than or equal to it.
The estimation lemma is most commonly used as part of the methods of contour integration
with the intent to show that the integral over part of a contour goes to zero as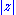
goes to infinity. An example of such a case is shown below.
Problem.
Find an upper bound for
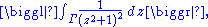
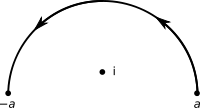
where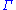
is the upper half-circle
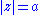with radius
traversed once in the counterclockwise direction.
Solution.
First observe that the length of the path of integration is half the circumference
of a circle with radius a, hence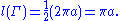
Next we seek an upper bound M for the integrand when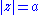
. By the triangle inequality
we see that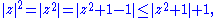
therefore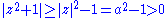
because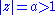
on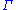 
.
Hence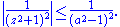
Therefore we apply the estimation lemma with M = 1 / (a2 − 1)2. The resulting bound is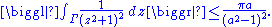
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
for a contour integral. If f is a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued, continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the contour
and if its absolute value |f(z)| is bounded by a constant M for all z on , then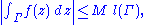where
is the arc lengthArc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of
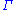. In particular, we may take the maximumMaxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
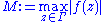
as upper bound. Intuitively, the lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
is very simple to understand. If a contour is thought of as many smaller contour segments connected together, then there will be a maximum |f(z)| for each segment. Out of all the maximum |f(z)|'s for the segments, there will be an overall largest one. Hence, if the overall largest |f(z)| is summed over the entire path then the integral of f(z) over the path must be less than or equal to it.
The estimation lemma is most commonly used as part of the methods of contour integration
Methods of contour integration
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
with the intent to show that the integral over part of a contour goes to zero as
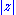goes to infinity. An example of such a case is shown below.Example
Find an upper bound for
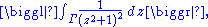
where
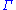is the upper half-circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
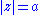with radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
traversed once in the counterclockwise direction.Solution.
First observe that the length of the path of integration is half the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of a circle with radius a, hence
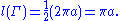
Next we seek an upper bound M for the integrand when
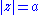. By the triangle inequalityTriangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
we see that
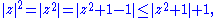
therefore
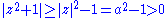
because
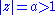on 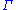.Hence
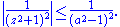
Therefore we apply the estimation lemma with M = 1 / (a2 − 1)2. The resulting bound is