
Exact test
Encyclopedia
In statistics
, an exact (significance) test is a test where all assumptions upon which the derivation of the distribution of the test statistic
is based are met, as opposed to an approximate test, in which the approximation may be made as close as desired by making the sample size big enough. This will result in a significance test that will have a false rejection rate always equal to the significance level of the test. For example an exact test at significance level 5% will in the long run reject true null hypothesis
exactly 5% of the time.
Parametric
tests, such as those described in exact statistics
, are exact tests when the parametric assumptions are fully met, but in practice the use of the term exact (significance) test is reserved for those tests that do not rest on parametric assumptions – non-parametric tests. However, in practice most implementations of non-parametric test software use asymptotical algorithms for obtaining the significance value, which makes the implementation of the test non-exact.
So when the result of a statistical analysis is said to be an “exact test” or an “exact p-value
”, it ought to imply that the test is defined without parametric assumptions and evaluated without using approximate algorithms. In principle however it could also mean that a parametric test has been employed in a situation where all parametric assumptions are fully met, but it is in most cases impossible to prove this completely in a real world situation. Exceptions when it is certain that parametric tests are exact include tests based on the binomial or Poisson distributions. Sometimes permutation test is used as a synonym for exact test, but although all permutation tests are exact tests, not all exact tests are permutation tests.
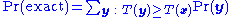
where:
and where the sum ranges over all outcomes y (including the observed one) that have the same value of the test statistic obtained for the observed sample x, or a larger one .
is an approximate test. Suppose Pearson's chi-squared test is used to ascertain whether a six-sided die is "fair", i.e. gives each of the six outcomes equally often. If the die is thrown n times, then one "expects"
to see each outcome n/6 times. The test statistic is
where Xk is the number of times outcome k is observed. If the null hypothesis of "fairness" is true, then the probability distribution
of the test statistic can be made as close as desired to the chi-squared distribution with5 degrees of freedom by making the sample size n big enough. But if n is small, then the probabilities based on chi-squared distributions may not be very close approximations. Finding the exact probability that this test statistic exceeds a certain value then requires combinatorial enumeration
of all outcomes of the experiment that result in such a large value of the test statistic. Moreover, it becomes questionable whether the same test statistic ought to be used. A likelihood-ratio test
might be preferred as being more powerful
, and the test statistic might not be a monotone function of the one above.
is exact because the sampling distribution (conditional on the marginals) is known exactly. Compare Pearson's chi-squared test
, which (although it tests the same null) is not exact because the distribution of the test statistic is correct only asymptotically.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, an exact (significance) test is a test where all assumptions upon which the derivation of the distribution of the test statistic
Test statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
is based are met, as opposed to an approximate test, in which the approximation may be made as close as desired by making the sample size big enough. This will result in a significance test that will have a false rejection rate always equal to the significance level of the test. For example an exact test at significance level 5% will in the long run reject true null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
exactly 5% of the time.
Parametric
Parametric
Parametric may refer to:*Parametric equation*Parametric statistics*Parametric derivative*Parametric plot*Parametric model*Parametric oscillator *Parametric contract*Parametric insurance*Parametric feature based modeler...
tests, such as those described in exact statistics
Exact statistics
Exact statistics, such as that described in exact test, is a branch of statistics that was developed to provide more accurate results pertaining to statistical testing and interval estimation by eliminating procedures based on asymptotic and approximate statistical methods...
, are exact tests when the parametric assumptions are fully met, but in practice the use of the term exact (significance) test is reserved for those tests that do not rest on parametric assumptions – non-parametric tests. However, in practice most implementations of non-parametric test software use asymptotical algorithms for obtaining the significance value, which makes the implementation of the test non-exact.
So when the result of a statistical analysis is said to be an “exact test” or an “exact p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
”, it ought to imply that the test is defined without parametric assumptions and evaluated without using approximate algorithms. In principle however it could also mean that a parametric test has been employed in a situation where all parametric assumptions are fully met, but it is in most cases impossible to prove this completely in a real world situation. Exceptions when it is certain that parametric tests are exact include tests based on the binomial or Poisson distributions. Sometimes permutation test is used as a synonym for exact test, but although all permutation tests are exact tests, not all exact tests are permutation tests.
Definition
The basic equation underlying permutation tests is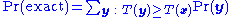
where:
- x is the outcome actually observed,
- Pr(y) is the probability under the null hypothesis of a potentially observed outcome y,
- T(y) is the value of the test statistic for an outcome y, with larger values of T representing cases which notionally represent greater departures from the null hypothesis,
and where the sum ranges over all outcomes y (including the observed one) that have the same value of the test statistic obtained for the observed sample x, or a larger one .
Example: Pearson's chi-squared test versus an exact test
A simple example of the occasion for this concept may be seen by observing that Pearson's chi-squared testPearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
is an approximate test. Suppose Pearson's chi-squared test is used to ascertain whether a six-sided die is "fair", i.e. gives each of the six outcomes equally often. If the die is thrown n times, then one "expects"
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
to see each outcome n/6 times. The test statistic is
where Xk is the number of times outcome k is observed. If the null hypothesis of "fairness" is true, then the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the test statistic can be made as close as desired to the chi-squared distribution with
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
of all outcomes of the experiment that result in such a large value of the test statistic. Moreover, it becomes questionable whether the same test statistic ought to be used. A likelihood-ratio test
Likelihood-ratio test
In statistics, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which is a special case of the other . The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other...
might be preferred as being more powerful
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
, and the test statistic might not be a monotone function of the one above.
Example: Fisher's exact test
Fisher's exact testFisher's exact test
Fisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
is exact because the sampling distribution (conditional on the marginals) is known exactly. Compare Pearson's chi-squared test
Pearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
, which (although it tests the same null) is not exact because the distribution of the test statistic is correct only asymptotically.


