
Expenditure minimization problem
Encyclopedia
In microeconomics
, the expenditure minimization problem is another perspective on the utility maximization problem
: "how much money do I need to reach a certain level of happiness?". This question comes in two parts. Given a consumer's utility function, prices, and a utility target,
is defined as follows. Suppose the consumer has a utility function defined on
defined on  commodities. Then the consumer's expenditure function gives the amount of money required to buy a package of commodities at given prices
commodities. Then the consumer's expenditure function gives the amount of money required to buy a package of commodities at given prices  that give utility of at least
that give utility of at least 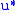 ,
,

where
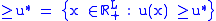
is the set of all packages that give utility at least as good as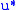 .
.
 is defined as the cheapest package that gives the desired utility. It can be defined in terms of the expenditure function with the Marshallian demand function
is defined as the cheapest package that gives the desired utility. It can be defined in terms of the expenditure function with the Marshallian demand function
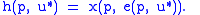
The relationship between the utility function and Marshallian demand in the Utility Maximization Problem mirrors the relationship between the expenditure function
and Hicksian demand in the Expenditure Minimization Problem
. It is also possible that the Hicksian and Marshallian demand are not unique (i.e. there is more than one commodity bundle that satisfies the expenditure minimization problem), then the demand is a correspondence
, and not a function. This does not happen, and the demands are functions, under the assumption of local nonsatiation
.
Microeconomics
Microeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...
, the expenditure minimization problem is another perspective on the utility maximization problem
Utility maximization problem
In microeconomics, the utility maximization problem is the problem consumers face: "how should I spend my money in order to maximize my utility?" It is a type of optimal decision problem.-Basic setup:...
: "how much money do I need to reach a certain level of happiness?". This question comes in two parts. Given a consumer's utility function, prices, and a utility target,
- how much money would the consumer need? This is answered by the expenditure functionExpenditure functionIn microeconomics, the expenditure function describes the minimum amount of money an individual needs to achieve some level of utility, given a utility function and prices....
. - what could the consumer buy to meet this utility target while minimizing expenditure? This is answered by the Hicksian demand functionHicksian demand functionIn microeconomics, a consumer's Hicksian demand correspondence is the demand of a consumer over a bundle of goods that minimizes their expenditure while delivering a fixed level of utility. If the correspondence is actually a function, it is referred to as the Hicksian demand function, or...
.
Expenditure function
Formally, the expenditure functionExpenditure function
In microeconomics, the expenditure function describes the minimum amount of money an individual needs to achieve some level of utility, given a utility function and prices....
is defined as follows. Suppose the consumer has a utility function
 defined on
defined on  commodities. Then the consumer's expenditure function gives the amount of money required to buy a package of commodities at given prices
commodities. Then the consumer's expenditure function gives the amount of money required to buy a package of commodities at given prices  that give utility of at least
that give utility of at least 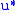 ,
,
where
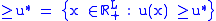
is the set of all packages that give utility at least as good as
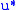 .
.Hicksian demand correspondence
Secondly, the Hicksian demand function is defined as the cheapest package that gives the desired utility. It can be defined in terms of the expenditure function with the Marshallian demand function
is defined as the cheapest package that gives the desired utility. It can be defined in terms of the expenditure function with the Marshallian demand functionMarshallian demand function
In microeconomics, a consumer's Marshallian demand function specifies what the consumer would buy in each price and wealth situation, assuming it perfectly solves the utility maximization problem...
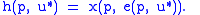
The relationship between the utility function and Marshallian demand in the Utility Maximization Problem mirrors the relationship between the expenditure function
Expenditure function
In microeconomics, the expenditure function describes the minimum amount of money an individual needs to achieve some level of utility, given a utility function and prices....
and Hicksian demand in the Expenditure Minimization Problem
Expenditure minimization problem
In microeconomics, the expenditure minimization problem is another perspective on the utility maximization problem: "how much money do I need to reach a certain level of happiness?". This question comes in two parts...
. It is also possible that the Hicksian and Marshallian demand are not unique (i.e. there is more than one commodity bundle that satisfies the expenditure minimization problem), then the demand is a correspondence
Correspondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
, and not a function. This does not happen, and the demands are functions, under the assumption of local nonsatiation
Local nonsatiation
The property of local nonsatiation of consumer preferences states that for any bundle of goods there is always another bundle of goods arbitrarily close that is preferred to it....
.

