Exponentially closed field
Encyclopedia
In mathematics
, an exponentially closed field is an ordered field
which has an order preserving isomorphism
of the additive group of 
onto the multiplicative group of positive elements of 
such that
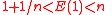for some natural number 
.
Isomorphism
is called an exponential function in 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an exponentially closed field is an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
which has an order preserving isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of the additive group of onto the multiplicative group of positive elements of such that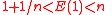 for some natural number .Isomorphism
is called an exponential function in .Examples
- The canonical example for an exponentially closed field is the ordered field of real numbers; here
can be any function 
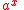where 
.
Properties
- Every exponentially closed field
is root-closed, i.e., every positive element of 
has an 
-th root for all positive integer 
(or in other words the multiplicative group of positive elements of 
is divisibleDivisible groupIn mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
). This is so because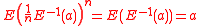
for all 
. - Consequently, every exponentially closed field is an Euclidean fieldEuclidean fieldIn mathematics, a Euclidean field is an ordered field K for which every non-negative element is a square: that is, x ≥ 0 in K implies that x = y2 for some y in K.-Properties:...
. - Consequently, every exponentially closed field is an ordered Pythagorean fieldPythagorean fieldIn algebra, a Pythagorean field is a field in which every sum of two squares is a square. A Pythagorean extension of a field F is an extension obtained by adjoining an element for some λ in F. So a Pythagorean field is one closed under taking Pythagorean extensions...
. - Not every real-closed field is an exponentially closed field, e.g., the field of real algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s is not exponentially closed. This is so because
has to be 
for some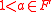 
in every exponentially closed subfield 
of the real numbers; and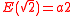 
is not algebraic if 
is algebraic by Gelfond–Schneider theoremGelfond–Schneider theoremIn mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
. - Consequently, the class of exponentially closed fields is not an elementary classElementary classIn the branch of mathematical logic called model theory, an elementary class is a class consisting of all structures satisfying a fixed first-order theory.- Definition :...
since the field of real numbers and the field of real algebraic numbers are elementarily equivalent structures. - The class of exponentially closed fields is a pseudoelementary classPseudoelementary classIn logic, a pseudoelementary class is a class of structures derived from an elementary class by omitting some of its sorts and relations. It is the mathematical logic counterpart of the notion in category theory of a forgetful functor, and in physics of hidden variable theories purporting to...
. This is so since a field
is exponentially closed iff there is a surjective function 
such that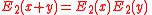 
and 
; and these properties of 
are axiomatizable.
See also
- Ordered exponential fields
- Exponential fieldsExponential fieldIn mathematics, an exponential field is a field that has an extra operation on its elements which extends the usual idea of exponentiation.-Definition:...