
Exponential field
Encyclopedia
In mathematics
, an exponential field is a field
that has an extra operation on its elements which extends the usual idea of exponentiation
.
under both operations with identities 0F and 1F respectively, and such that multiplication is distributive over addition, that is for any elements a, b, c in F, one has a · (b + c) = (a · b) + (a · c). If there is also a function
E that maps F into F, and such that for every a and b in F one has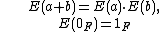
then F is called an exponential field, and the function E is called an exponential function on F. Thus an exponential function on a field is a homomorphism
from the additive group of F to its multiplicative group.
Hence, taking into account the Frobenius endomorphism
,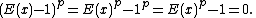
And so E(x) = 1 for every x. For this reason, exponential fields are sometimes required to have characteristic zero.
When the field does have characteristic zero then there can be non-trivial exponential functions.
, occasionally providing a link between it and number theory
as in the case of Zilber's work on Schanuel's conjecture
. It was proved in the 1990s that Rexp is model complete
, a result known as Wilkie's theorem
. This result, when combined with Khovanskiĭ's theorem on pfaffian function
s, proves that Rexp is also o-minimal. On the other hand it is known that Cexp is not model complete. The question of decidability
is still unresolved. Alfred Tarski
posed the question of the decidability of Rexp and hence it is now known as Tarski's exponential function problem
. It is known that if the real version of Schanuel's conjecture is true then Rexp is decidable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an exponential field is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
that has an extra operation on its elements which extends the usual idea of exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
.
Definition
A field is an algebraic structure composed of a set of elements, F, and two operations, addition ('+') and multiplication ('·'), such that the set of elements forms an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under both operations with identities 0F and 1F respectively, and such that multiplication is distributive over addition, that is for any elements a, b, c in F, one has a · (b + c) = (a · b) + (a · c). If there is also a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
E that maps F into F, and such that for every a and b in F one has
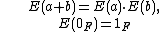
then F is called an exponential field, and the function E is called an exponential function on F. Thus an exponential function on a field is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from the additive group of F to its multiplicative group.
Examples
There is a trivial exponential function on any field, that is the map E that sends every element to 1F, the identity element of the field under multiplication. Thus every field is trivially also an exponential field, so the cases of interest to mathematicians occur when the exponential function is non-trivial.- If a field has characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
p > 0 then it can be shown that the only exponential function on the field is the trivial one. To see this first note that for any element x in the field,
Hence, taking into account the Frobenius endomorphism
Frobenius endomorphism
In commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
,
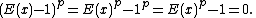
And so E(x) = 1 for every x. For this reason, exponential fields are sometimes required to have characteristic zero.
When the field does have characteristic zero then there can be non-trivial exponential functions.
- The field of real numbers R, or (R,+,·,0,1) as it may be written to highlight that we are considering it purely as a field with addition, multiplication, and special constants zero and one, has infinitely many exponential functions. One such function is the usual exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, that is E(x) = eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
x, since we have ex+y = exey and e0 = 1, as required. Considering the ordered fieldOrdered fieldIn mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
R equipped with this function gives the ordered real exponential field, denoted Rexp = (R,+,·,<,0,1,exp).
- In fact any real number a > 0 gives an exponential function on R, specifically the map E(x) = ax satisfies the required properties.
- Analogously to the real exponential field, there is the complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
exponential field, Cexp = (C,+,·,0,1,exp).
- Boris Zilber constructed an exponential field Kexp that, crucially, satisfies the equivalent formulation of Schanuel's conjectureSchanuel's conjectureIn mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
with the field's exponential function. It is conjectured that this exponential field is actually Cexp, and a proof of this fact would thus prove Schanuel's conjecture.
- The underlying set F may not be required to be a field but instead allowed to simply be a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, R, and concurrently the exponential function is relaxed to be a homomorphism from the additive group in R to the multiplicative group of unitsUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in R. The resulting object is called an exponential ring.
- An example of an exponential ring with a nontrivial exponential function is the ring of integers Z equipped with the function E which takes the value +1 at even integers and −1 at odd integers, i.e., the function
 This exponential function, and the trivial one, are the only two functions on Z that satisfy the conditions.
This exponential function, and the trivial one, are the only two functions on Z that satisfy the conditions.
Open problems
Exponential fields are a much-studied object in model theoryModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, occasionally providing a link between it and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
as in the case of Zilber's work on Schanuel's conjecture
Schanuel's conjecture
In mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
. It was proved in the 1990s that Rexp is model complete
Model complete theory
In model theory, a first-order theory is called model complete if every embedding of models is an elementary embedding.Equivalently, every first-order formula is equivalent to a universal formula.This notion was introduced by Abraham Robinson....
, a result known as Wilkie's theorem
Wilkie's theorem
In mathematics, Wilkie's theorem is a result by Alex Wilkie about the theory of ordered fields with an exponential function, or equivalently about the geometric nature of exponential varieties.-Formulations:...
. This result, when combined with Khovanskiĭ's theorem on pfaffian function
Pfaffian function
In mathematics, the Pfaffian functions are a certain class of functions introduced by Askold Georgevich Khovanskiǐ in the 1970s. They are named after German mathematician Johann Pfaff.-Basic definition:...
s, proves that Rexp is also o-minimal. On the other hand it is known that Cexp is not model complete. The question of decidability
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
is still unresolved. Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
posed the question of the decidability of Rexp and hence it is now known as Tarski's exponential function problem
Tarski's exponential function problem
In model theory, Tarski's exponential function problem asks whether the usual theory of the real numbers together with the exponential function is decidable...
. It is known that if the real version of Schanuel's conjecture is true then Rexp is decidable.

