
Extended Kalman filter
Encyclopedia
In estimation theory
, the extended Kalman filter (EKF) is the nonlinear version of the Kalman filter
which linearizes about the current mean and covariance. The EKF has been considered the de facto
standard in the theory of nonlinear state estimation, navigation system
s and GPS.
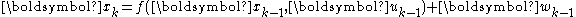
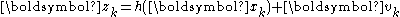
Where wk and vk are the process and observation noises which are both assumed to be zero mean multivariate Gaussian noises with covariance
Qk and Rk respectively.
The function f can be used to compute the predicted state from the previous estimate and similarly the function h can be used to compute the predicted measurement from the predicted state. However, f and h cannot be applied to the covariance directly. Instead a matrix of partial derivatives (the Jacobian) is computed.
At each timestep the Jacobian is evaluated with current predicted states. These matrices can be used in the Kalman filter equations. This process essentially linearizes the non-linear function around the current estimate.
where the state transition and observation matrices are defined to be the following Jacobians
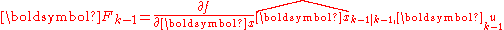
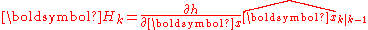

Initialize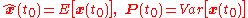
Predict-Update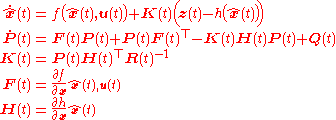
Unlike discrete-time extended Kalman filter, the prediction and update steps are coupled in continuous-time extended Kalman filter.
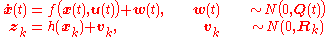
where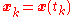 .
.
Initialize
Predict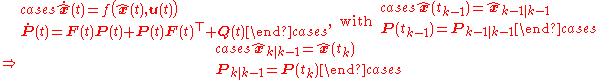
where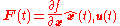
Update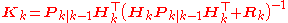
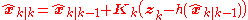
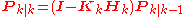
where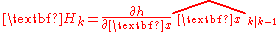
The update equations are identical to those of discrete-time extended Kalman filter.
Having stated this, the extended Kalman filter can give reasonable performance, and is arguably the de facto
standard in navigation systems and GPS.
(IEKF) is a modified version of the EKF for nonlinear systems possessing symmetries (or invariances). It combines the advantages of both the EKF and the recently introduced symmetry-preserving filters. Indeed, instead of using a linear correction term based on a linear output error, it uses a geometrically adapted correction term based on an invariant output error; in the same way the gain matrix is not updated from a linear state error, but from an invariant state error. The main benefit is that the gain and covariance equations converge to constant values on a much bigger set of trajectories than equilibrium points as it is the case for the EKF, which results in a better convergence of the estimation.
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
, the extended Kalman filter (EKF) is the nonlinear version of the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
which linearizes about the current mean and covariance. The EKF has been considered the de facto
De facto
De facto is a Latin expression that means "concerning fact." In law, it often means "in practice but not necessarily ordained by law" or "in practice or actuality, but not officially established." It is commonly used in contrast to de jure when referring to matters of law, governance, or...
standard in the theory of nonlinear state estimation, navigation system
Navigation system
A navigation system is a system that aids is navigation. Navigation systems may be entirely on board a vehicle or vessel, or they may be located elsewhere and communicate via radio or other signals with a vehicle or vessel, or they may use a combination of these methods.Navigation systems may be...
s and GPS.
Formulation
In the extended Kalman filter, the state transition and observation models need not be linear functions of the state but may instead be differentiable functions.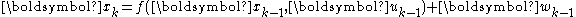
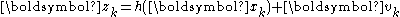
Where wk and vk are the process and observation noises which are both assumed to be zero mean multivariate Gaussian noises with covariance
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
Qk and Rk respectively.
The function f can be used to compute the predicted state from the previous estimate and similarly the function h can be used to compute the predicted measurement from the predicted state. However, f and h cannot be applied to the covariance directly. Instead a matrix of partial derivatives (the Jacobian) is computed.
At each timestep the Jacobian is evaluated with current predicted states. These matrices can be used in the Kalman filter equations. This process essentially linearizes the non-linear function around the current estimate.
Predict
| Predicted state estimate | 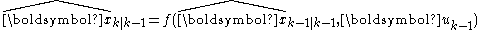 |
Predicted estimate covariance |  |
Update
| Innovation or measurement residual |  |
| Innovation (or residual) covariance | 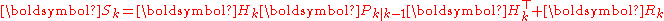 |
| Near-Optimal Kalman gain | 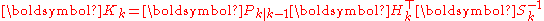 |
| Updated state estimate | 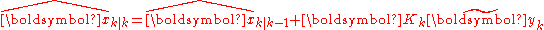 |
| Updated estimate covariance |  |
where the state transition and observation matrices are defined to be the following Jacobians
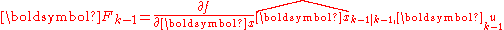
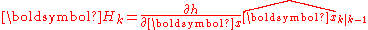
Continuous-time extended Kalman filter
Model
Initialize
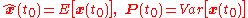
Predict-Update
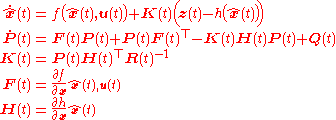
Unlike discrete-time extended Kalman filter, the prediction and update steps are coupled in continuous-time extended Kalman filter.
Continuous-discrete extended Kalman filter
Most physical systems are represented as continuous-time models while discrete-time measurements are frequently taken for state estimation via a digital processor. Therefore, the system model and measurement model are given by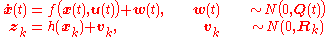
where
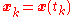 .
.Initialize

Predict
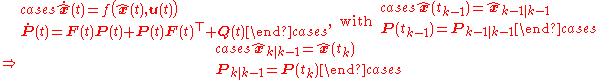
where
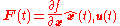
Update
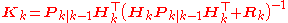
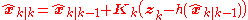
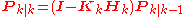
where
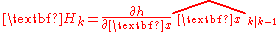
The update equations are identical to those of discrete-time extended Kalman filter.
Disadvantages of the extended Kalman filter
Unlike its linear counterpart, the extended Kalman filter in general is not an optimal estimator (of course it is optimal if the measurement and the state transition model are both linear, as in that case the extended Kalman filter is identical to the regular one). In addition, if the initial estimate of the state is wrong, or if the process is modeled incorrectly, the filter may quickly diverge, owing to its linearization. Another problem with the extended Kalman filter is that the estimated covariance matrix tends to underestimate the true covariance matrix and therefore risks becoming inconsistent in the statistical sense without the addition of "stabilising noise".Having stated this, the extended Kalman filter can give reasonable performance, and is arguably the de facto
De facto
De facto is a Latin expression that means "concerning fact." In law, it often means "in practice but not necessarily ordained by law" or "in practice or actuality, but not officially established." It is commonly used in contrast to de jure when referring to matters of law, governance, or...
standard in navigation systems and GPS.
Unscented Kalman filters
An improvement to the extended Kalman filter led to the development of the Unscented Kalman filter (UKF), also a nonlinear filter. In the UKF, the probability density is approximated by the nonlinear transformation of a random variable, which returns much more accurate results than the first-order Taylor expansion of the nonlinear functions in the EKF. The approximation utilizes a set of sample points, which guarantees accuracy with the posterior mean and covariance to the second order for any nonlinearity. The UKF tends to be more robust and more accurate than the EKF in its estimation of error.
"The extended Kalman filter (EKF) is probably the most widely used estimation algorithm for nonlinear systems. However, more than 35 years of experience in the estimation community has shown that is difficult to implement, difficult to tune, and only reliable for systems that are almost linear on the time scale of the updates. Many of these difficulties arise from its use of linearization."
Invariant extended Kalman filter
The invariant extended Kalman filterInvariant extended Kalman filter
The invariant extended Kalman filter is a new version of the extended Kalman filter for nonlinear systems possessing symmetries . It combines the advantages of both the EKF and the recently introduced symmetry-preserving filters...
(IEKF) is a modified version of the EKF for nonlinear systems possessing symmetries (or invariances). It combines the advantages of both the EKF and the recently introduced symmetry-preserving filters. Indeed, instead of using a linear correction term based on a linear output error, it uses a geometrically adapted correction term based on an invariant output error; in the same way the gain matrix is not updated from a linear state error, but from an invariant state error. The main benefit is that the gain and covariance equations converge to constant values on a much bigger set of trajectories than equilibrium points as it is the case for the EKF, which results in a better convergence of the estimation.
See also
- Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
- Invariant extended Kalman filterInvariant extended Kalman filterThe invariant extended Kalman filter is a new version of the extended Kalman filter for nonlinear systems possessing symmetries . It combines the advantages of both the EKF and the recently introduced symmetry-preserving filters...
- Unscented Kalman filter
- Ensemble Kalman filterEnsemble Kalman filterThe ensemble Kalman filter is a recursive filter suitable for problems with a large number of variables, such as discretizations of partial differential equations in geophysical models...
- Fast Kalman filterFast Kalman filterThe fast Kalman filter , devised by Antti Lange , is an extension of the Helmert-Wolf blocking method from geodesy to real-time applications of Kalman filtering such as satellite imaging of the Earth...
- Masreliez’s theorem
- Particle filterParticle filterIn statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...

