Fedor Bogomolov
Encyclopedia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
and American mathematician, known for his research in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. Bogomolov worked at Steklov Institute
Steklov Institute of Mathematics
Steklov Institute of Mathematics or Steklov Mathematical Institute is a research institute based in Moscow, specialized in mathematics, and a part of the Russian Academy of Sciences. It was established April 24, 1934 by the decision of the General Assembly of the Academy of Sciences of the USSR in...
in Moscow before he became a professor at Courant Institute. He is most famous for his pioneering work on hyperkähler manifold
Hyperkähler manifold
In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...
s.
Born in Moscow, Bogomolov graduated from Moscow State University
Moscow State University
Lomonosov Moscow State University , previously known as Lomonosov University or MSU , is the largest university in Russia. Founded in 1755, it also claims to be one of the oldest university in Russia and to have the tallest educational building in the world. Its current rector is Viktor Sadovnichiy...
, Faculty of Mechanics and Mathematics, and earned his doctorate ("candidate degree") in 1973, in Steklov Institute
Steklov Institute of Mathematics
Steklov Institute of Mathematics or Steklov Mathematical Institute is a research institute based in Moscow, specialized in mathematics, and a part of the Russian Academy of Sciences. It was established April 24, 1934 by the decision of the General Assembly of the Academy of Sciences of the USSR in...
. His advisor was Sergei Novikov.
Geometry of Kähler manifoldKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s
Bogomolov's Ph. D. was entitled Compact Kähler varieties. In his early papers Bogomolov studied the manifolds which were later called Calabi-Yau and hyperkaehler. He proved a decomposition theorem, used for the classification of manifolds with trivial canonical class. It has been re-proven using the Calabi-Yau theorem and Berger's classification of Riemannian holonomiesHolonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
, and is foundational for modern string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
.
In the late 1970s and early 1980s Bogomolov studied the deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
for manifolds with trivial canonical class. He discovered what is now known as Bogomolov-Tian-Todorov theorem, proving the smoothness and un-obstructedness of the deformation space for hyperkaehler manifolds (in 1978 paper) and then extended this to all Calabi-Yau manifolds in the 1981 IHES preprint. Some years later, this theorem became the mathematical foundation for Mirror Symmetry
Mirror symmetry
In physics and mathematics, mirror symmetry is a relation that can exist between two Calabi-Yau manifolds. It happens, usually for two such six-dimensional manifolds, that the shapes may look very different geometrically, but nevertheless they are equivalent if they are employed as hidden...
.
While studying the deformation theory of hyperkaehler manifolds, Bogomolov discovered what is now known as Bogomolov-Beauville-Fujiki form on
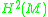.Studying properties of this form, Bogomolov erroneously concluded that compact hyperkaehler manifolds don't exist, with exception of a K3 surface
K3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
, torus and their products. Almost 4 years passed since this publication before Fujiki found a counterexample.
Other works in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
Bogomolov's most-cited paper is"Holomorphic tensors and vector bundles on projective manifolds." He proved what is now known as Bogomolov-Miyaoka-Yau inequality and defined a new, refined notion of stability for holomorphic vector bundles (Bogomolov stability). Bogomolov also proved that a stable bundle on a surface, restricted to a curve of sufficiently big degree, remains stable.
In another seminal paper, "Families of curves on a surface of general type", Bogomolov laid the foundations to the now popular approach to the theory of diophantine equations through geometry of hyperbolic manifolds and dynamical systems. In this paper Bogomolov proved that on any surface of general type
Surface of general type
In algebraic geometry, a surface of general type is an algebraic surface with Kodaira dimension 2. Because of Chow's theorem any compact complex manifold of dimension 2 and with Kodaira dimension 2 will actually be an algebraic surface, and in some sense most surfaces are in this...
with
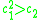, there is only a finite number of curves of bounded genus. Some 25 years later, Michael McQuillan extended this argument to prove the famous Green-Griffiths conjecturefor such surfaces.
Another remarkable paper is "Classification of surfaces of class
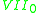with 
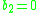", Using affine structures on complex manifolds, Bogomolov made the first step in a famously difficult (and still unresolved) problem of classification of surfaces of Kodaira class VII. These are compact complex surfaces with 
. If they are in addition minimal, they are called class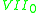 
. Kodaira classified all compact complex surfaces except class VII, which are still not understood, except the case 
(Bogomolov) and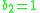 
(A. Teleman, 2005).Later career
Bogomolov obtained his Habilitation (Russian "Dr. of Sciences") in 1983. In 1994, he emigrated to the U.S. and became a full professor at the Courant Institute. He is very active in algebraic geometry and number theory. In 2006, Bogomolov turned 60; two major conferences commemorating his birthday were held - one at the University of Miami, and another in Moscow, Steklov Institute. From 2009 he serves as the Editor-in-Chief of Central European Journal of MathematicsCentral European Journal of Mathematics
The Central European Journal of Mathematics is a peer-reviewed bimonthly scientific journal covering all areas of mathematics. It was established in 2003 and is published by Versita in collaboration with Springer Science+Business Media....
.
External links
- Official NYU home page
- Новые перспективы науки Nov. 2, 2006, Bilingua club, Moscow.
- "Из научной интеллигенции можно сформировать "сословие экспертов" An interview of Fedor Bogomolov (Olga Orlova for polit.ru)