Fenchel's duality theorem
Encyclopedia
In mathematics, Fenchel's duality theorem is a result in the theory of convex functions named after Werner Fenchel
.
Let ƒ be a proper convex function
on Rn and let g be a proper concave function on Rn. Then, if regularity conditions are satisfied,
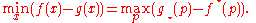
where ƒ * is the convex conjugate
of ƒ (also referred to as the Fenchel–Legendre transform) and g * is the concave conjugate of g. That is,
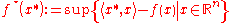
and 
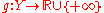be convex functions and 
be a bounded
linear map. Then the Fenchel problems: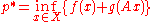
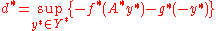
satisfy weak duality, i.e.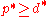
. Note that 
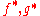are the convex conjugates of f,g respectively, and 
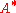is the adjoint operator. The perturbation function
for this dual problem
is given by
.
Suppose that f,g, and A satisfy either
Then strong duality holds, i.e.
. If 
then supremum
is attained.
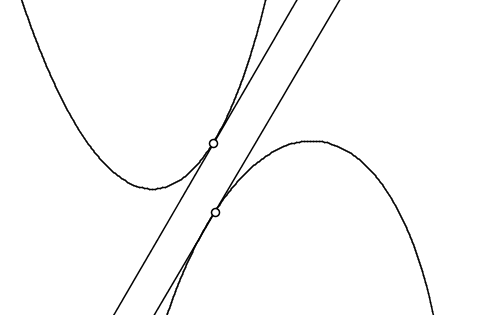
The next figure illustrates the maximization problem on the right hand side of the above equation. Tangents are drawn to each of the two curves such that both tangents have the same slope p. The problem is to adjust p in such a way that the two tangents are as far away from each other as possible (more precisely, such that the point where they intersect the y-axis are as far from each other as possible). Imagine the two tangents as metal bars with vertical springs between them that push them apart and against the two parabolas that are fixed in place.
Fenchel's theorem states that the two problems have the same solution. The points having the minimum vertical separation are also the tangency points for the maximally separated parallel tangents.
Werner Fenchel
Moritz Werner Fenchel was a mathematician known for his contributions to geometry and to optimization theory. Fenchel established the basic results of convex analysis and nonlinear optimization theory. Fenchel's monographs and lecture-notes were very influential also...
.
Let ƒ be a proper convex function
Proper convex function
In mathematical analysis and optimization, a proper convex function is a convex function f taking values in the extended real number line such thatf -\infty...
on Rn and let g be a proper concave function on Rn. Then, if regularity conditions are satisfied,
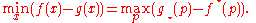
where ƒ * is the convex conjugate
Convex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
of ƒ (also referred to as the Fenchel–Legendre transform) and g * is the concave conjugate of g. That is,
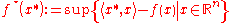
Mathematical theorem
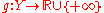Let X and Y be Banach spaces, and be convex functions and be a boundedBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
linear map. Then the Fenchel problems:
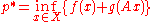
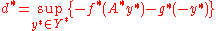
satisfy weak duality, i.e.
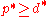. Note that 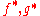are the convex conjugates of f,g respectively, and 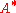is the adjoint operator. The perturbation functionPerturbation function
In mathematical optimization, the perturbation function is any function which relates to primal and dual problems. The name comes from the fact that any such function defines a perturbation of the initial problem...
for this dual problem
Dual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
is given by
.Suppose that f,g, and A satisfy either
- f and g are lower semi-continuous and
where 
is the algebraic interiorAlgebraic interiorIn functional analysis, a branch of mathematics, the algebraic interior or radial kernel of a subset of a vector space is a refinement of the concept of the interior. It is the subset of points contained in a given set that it is absorbing with respect to, i.e...
and
where h is some function is the set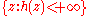 
, or -
where 
are the points where the function is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
Then strong duality holds, i.e.
. If then supremumSupremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is attained.
One-dimensional illustration
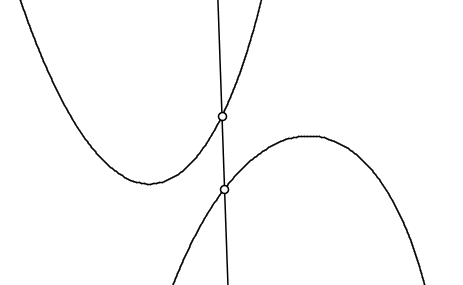
In the following figure, the minimization problem on the left side of the equation is illustrated. One seeks to vary x such that the vertical distance between the convex and concave curves at x is as small as possible. The position of the vertical line in the figure is the (approximate) optimum.The next figure illustrates the maximization problem on the right hand side of the above equation. Tangents are drawn to each of the two curves such that both tangents have the same slope p. The problem is to adjust p in such a way that the two tangents are as far away from each other as possible (more precisely, such that the point where they intersect the y-axis are as far from each other as possible). Imagine the two tangents as metal bars with vertical springs between them that push them apart and against the two parabolas that are fixed in place.
Fenchel's theorem states that the two problems have the same solution. The points having the minimum vertical separation are also the tangency points for the maximally separated parallel tangents.