Feynman-Wheeler theory
Encyclopedia
The Wheeler–Feynman absorber theory (also called the Wheeler–Feynman Time-Symmetric theory) is an interpretation of electrodynamics that starts from the idea that a solution to the electromagnetic field equations has to be symmetric with respect to time-inversion, as are the field equations themselves. The motivation for such choice is mainly due to the importance that time symmetry has in physics. Indeed, there is no apparent reason for which such symmetry should be broken, and therefore one time direction has no privilege to be more important than the other. Thus, a theory that respects this symmetry appears more elegant than theories with which one has to arbitrarily choose one time direction over the other as the preferred one. Another key idea reminiscent of Mach's principle
due to Tetrode
is that elementary particles act on other elementary particles not themselves; this immediately removes the problem of self-energies
. This theory is named after its originators, the late physicists Richard Feynman
and John Archibald Wheeler
.
. Maxwell's equations
and the wave equation for electromagnetic waves have, in general, two possible solutions: a retarded solution and an advanced one. This means that if we have an electromagnetic emitter which generates a wave at
time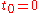
and point 
, then the wave of the first solution will arrive at point 
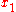at the instant 
after the emission (where 
is the speed of light) while the second one will arrive at the same place at the instant 
before the emission. The second wave appears to be clearly unphysical as it means that in a model where it is considered we could see the effect of any phenomenon before it happens, and therefore it is usually discarded in the interpretation of electromagnetic waves.
Feynman and Wheeler overcame this difficulty in a very simple way. Consider all the emitters which are present in our universe, then if all of them generate electromagnetic waves in a symmetric way, the resulting field is
Then, if you consider that in your universe holds the relation
you can freely add this last quantity to the total field solution of Maxwell equations
(being a solution of the homogenous Maxwell equation) and you get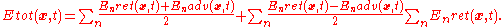
In this way the model sees just the effect of the retarded field, and so causality still holds. The presence of this free field is related to the phenomenon of the absorption from all the particles of the universe of the radiation emitted by each single particle. Still the idea is quite simple as it's the same phenomenon which happens when an electromagnetic wave is absorbed from an object; if you look to the process on a microscopic scale you will see that the absorption is due to the presence of the electromagnetic fields of all the electrons which react to the external perturbation and create fields which cancel it. The main difference here is that the process is allowed to happen with advanced waves.
Finally one could still consider that this formulation is still no more symmetric than the usual one as the retarded time direction still seems to be privileged. However, this is only an illusion as one can always reverse the process simply reversing who is considered as the emitter and who is considered the absorber. Any apparent 'privilege' of a time direction is only due to the arbitrary choice of which is the emitter and which the absorber.
If we consider the Lagrangian
acting on particle 1 from the time-symmetric fields generated by particle 2, we have: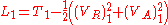
where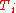
is the relativistic kinetic energy functional of particle i, 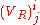and, 
and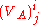 
are respectively the retarded and advanced Liénard–Wiechert potentials acting on particle j from the relativistic electromagnetic fields generated by particle i. Conversely, the corresponding Lagrangian for particle 2 motioned by particle 1 is: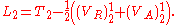
It was originally demonstrated with experimental mathematics
via computer algebra and then proven mathematically that the difference between a retarded potential of particle i acting on particle j and the advanced potential of particle j acting on particle i is simply a total time derivative: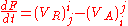
or a divergence as it is called in the Calculus of variations
because it contributes nothing to the Euler-Lagrange equation
s. Thus, by adding the right amount of total time derivatives to these Lagrangians, the advanced potentials can be eliminated. The Lagrangian for the N-body system is therefore: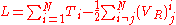
in which the advanced potentials make no appearance. Furthermore, this Lagrangian exhibits particle-particle symmetry. For
this Lagrangian will generate exactly the same equations of motion of 
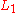and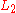 
and consequently the Physics of the problem is preserved. Therefore, from the point of view of an outside observer viewing the relativistic n-body problem
, everything is causal. However, if we isolate the forces acting on a particular body, the advanced potential makes its appearance. This recasting of the problem comes at a price: the N-body Lagrangian depends on all the time derivatives of the curves traced by all particles i.e. the Lagrangian is infinite order. Nonetheless, symmetry under exchange of particles and total Generalized momenta (resulting from the definition of an infinite order Lagrangian) are conserved. The one feature which might seem non-local is that Hamilton's principle
is applied to a relativistic many-particle system as a whole but this is as far as one can go with a classical (non quantum-mechanical) theory. However, much progress was made in examining the unresolved issue of quantizing the theory.
Numerical solutions for the classical problem were also found. Also note that this formulation recovers the Darwin Lagrangian from which the Breit equation
was originally derived but without the dissipative terms. This ensures agreement with theory and experiment up to but not including the Lamb shift.
), then is known that this particle radiates, and so loses energy. If you write down the Newton equation of the particle you need a damping term which takes into account this energy loss. The first solution to this problem is mainly due to Lorentz and was later expanded on by Dirac. Lorentz interpreted this loss as due to the retarded self-interaction of such a particle with its own field. Such interpretation though is not completely satisfactory as it leads to divergences in the theory and needs some assumption on the structure of charge distribution of the particle. Dirac generalized the formula given by Lorentz for the damping factor to make it relativistically invariant. While doing so, he also suggested a different interpretation of the damping factor as being due to the free fields acting on the particle at its own position.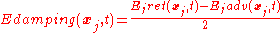
The main lack of this formulation is the absence of a physical justification for the presence of such fields.
So absorber theory was formulated as an attempt to correct this point. Using absorber theory, if we assume that each particle does not interact with itself and evaluate the field acting on the particle
at its own position (the point 
) we get:
It's clear that if we now add to this the free fields
we obtain
and so
This interpretation avoids the problem of divergent self-energy for a particle giving a reasonably physical interpretation to the equation of Dirac. Moore and Scott showed that the radiation reaction can be alternatively derived using the notion that on average the net dipole moment is zero for a collection of charged particles, thereby avoiding the complications of the absorber theory.
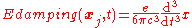
which is the Lorentz formulation. Since the third derivative with respect to the time appears here, it is clear that to solve the equation is not sufficient to give just the initial position and velocity of the particle, but the initial acceleration of the particle will also be needed, which makes no sense. This problem is solved by observing that the equation of motion for the particle has to be solved together with the Maxwell equations for the field generated by the particle itself. So instead of giving the initial acceleration one can give the initial field and the boundary condition. This restores the coherence of the physical interpretation of the theory. Still some difficulties may arise when one tries to solve the equation and interpret the solution. It is commonly stated that the Maxwell equations are classical and cannot correctly account for microscopic phenomena such as the behavior of a point-like particle where quantum mechanical effects should appear. However with absorber theory, Wheeler and Feynman were able to create a coherent classical approach to the problem.
When they formulated this paper Wheeler and Feynman were trying to avoid this divergent term. Later however, Feynman would come to state that self-interaction is needed as it correctly accounts, within quantum mechanics, for the Lamb shift. This theory is mentioned in the chapter entitled "Monster Minds" in Feynman's autobiographical work Surely You're Joking, Mr. Feynman!
as well as in Vol. II of the Feynman Lectures on Physics. It led to the formulation of a framework of quantum mechanics using a Lagrangian and action as starting point rather than a Hamiltonian, namely the formulation using Feynman Path integrals
which proved useful in Feynman's earliest calculations in quantum electrodynamics
and quantum field theory
in general. Both retarded and advanced fields appear respectively as retarded and advanced propagators, and also, in the Feynman propagator and the Dyson
propagator.
Mach's principle
In theoretical physics, particularly in discussions of gravitation theories, Mach's principle is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach....
due to Tetrode
Hugo Tetrode
Hugo Martin Tetrode was a Dutch theoretical physicist who contributed to statistical physics, early quantum theory and quantum mechanics....
is that elementary particles act on other elementary particles not themselves; this immediately removes the problem of self-energies
Self-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
. This theory is named after its originators, the late physicists Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
and John Archibald Wheeler
John Archibald Wheeler
John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
.
The problem of causality
The first problem one has to face if one wants to construct a time-symmetric theory is the problem of causalityCausality (physics)
Causality is the relationship between causes and effects. It is considered to be fundamental to all natural science, especially physics. Causality is also a topic studied from the perspectives of philosophy and statistics....
. Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and the wave equation for electromagnetic waves have, in general, two possible solutions: a retarded solution and an advanced one. This means that if we have an electromagnetic emitter which generates a wave at
time
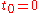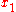and point , then the wave of the first solution will arrive at point at the instant after the emission (where is the speed of light) while the second one will arrive at the same place at the instant before the emission. The second wave appears to be clearly unphysical as it means that in a model where it is considered we could see the effect of any phenomenon before it happens, and therefore it is usually discarded in the interpretation of electromagnetic waves.Feynman and Wheeler overcame this difficulty in a very simple way. Consider all the emitters which are present in our universe, then if all of them generate electromagnetic waves in a symmetric way, the resulting field is
Then, if you consider that in your universe holds the relation
you can freely add this last quantity to the total field solution of Maxwell equations
(being a solution of the homogenous Maxwell equation) and you get
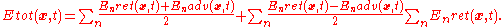
In this way the model sees just the effect of the retarded field, and so causality still holds. The presence of this free field is related to the phenomenon of the absorption from all the particles of the universe of the radiation emitted by each single particle. Still the idea is quite simple as it's the same phenomenon which happens when an electromagnetic wave is absorbed from an object; if you look to the process on a microscopic scale you will see that the absorption is due to the presence of the electromagnetic fields of all the electrons which react to the external perturbation and create fields which cancel it. The main difference here is that the process is allowed to happen with advanced waves.
Finally one could still consider that this formulation is still no more symmetric than the usual one as the retarded time direction still seems to be privileged. However, this is only an illusion as one can always reverse the process simply reversing who is considered as the emitter and who is considered the absorber. Any apparent 'privilege' of a time direction is only due to the arbitrary choice of which is the emitter and which the absorber.
Resolution of causality issue
T.C. Scott and R.A. Moore demonstrated that the apparent acausality caused by the presence of advanced Liénard–Wiechert potentials in their original formulation could be removed by recasting their theory into a fully relativistic many-bodied electrodynamics formulation in terms of retarded potentials only without the complications of the absorber part of the theory.If we consider the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
acting on particle 1 from the time-symmetric fields generated by particle 2, we have:
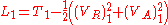
where
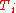is the relativistic kinetic energy functional of particle i, 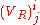and, and 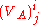are respectively the retarded and advanced Liénard–Wiechert potentials acting on particle j from the relativistic electromagnetic fields generated by particle i. Conversely, the corresponding Lagrangian for particle 2 motioned by particle 1 is: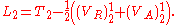It was originally demonstrated with experimental mathematics
Experimental mathematics
Experimental mathematics is an approach to mathematics in which numerical computation is used to investigate mathematical objects and identify properties and patterns...
via computer algebra and then proven mathematically that the difference between a retarded potential of particle i acting on particle j and the advanced potential of particle j acting on particle i is simply a total time derivative:
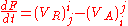
or a divergence as it is called in the Calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
because it contributes nothing to the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
s. Thus, by adding the right amount of total time derivatives to these Lagrangians, the advanced potentials can be eliminated. The Lagrangian for the N-body system is therefore:
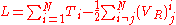
in which the advanced potentials make no appearance. Furthermore, this Lagrangian exhibits particle-particle symmetry. For
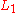this Lagrangian will generate exactly the same equations of motion of and 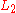and consequently the Physics of the problem is preserved. Therefore, from the point of view of an outside observer viewing the relativistic n-body problemN-body problem
The n-body problem is the problem of predicting the motion of a group of celestial objects that interact with each other gravitationally. Solving this problem has been motivated by the need to understand the motion of the Sun, planets and the visible stars...
, everything is causal. However, if we isolate the forces acting on a particular body, the advanced potential makes its appearance. This recasting of the problem comes at a price: the N-body Lagrangian depends on all the time derivatives of the curves traced by all particles i.e. the Lagrangian is infinite order. Nonetheless, symmetry under exchange of particles and total Generalized momenta (resulting from the definition of an infinite order Lagrangian) are conserved. The one feature which might seem non-local is that Hamilton's principle
Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
is applied to a relativistic many-particle system as a whole but this is as far as one can go with a classical (non quantum-mechanical) theory. However, much progress was made in examining the unresolved issue of quantizing the theory.
Numerical solutions for the classical problem were also found. Also note that this formulation recovers the Darwin Lagrangian from which the Breit equation
Breit equation
The Breit equation is a relativistic wave equation derived by Gregory Breit in 1929 based on the Dirac equation, which formally describes two or more massive spin-1/2 particles interacting electromagnetically to the first order in perturbation theory. It accounts for magnetic interactions and...
was originally derived but without the dissipative terms. This ensures agreement with theory and experiment up to but not including the Lamb shift.
The problem of self-interaction and damping
The motivation of finding a different interpretation of the electromagnetic phenomena comes even from the need for a satisfying description of the electromagnetic radiation process. The point here is the following: consider a charged particle that moves in a nonuniform way (for example an oscillating one), then is known that this particle radiates, and so loses energy. If you write down the Newton equation of the particle you need a damping term which takes into account this energy loss. The first solution to this problem is mainly due to Lorentz and was later expanded on by Dirac. Lorentz interpreted this loss as due to the retarded self-interaction of such a particle with its own field. Such interpretation though is not completely satisfactory as it leads to divergences in the theory and needs some assumption on the structure of charge distribution of the particle. Dirac generalized the formula given by Lorentz for the damping factor to make it relativistically invariant. While doing so, he also suggested a different interpretation of the damping factor as being due to the free fields acting on the particle at its own position.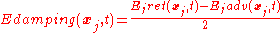The main lack of this formulation is the absence of a physical justification for the presence of such fields.
So absorber theory was formulated as an attempt to correct this point. Using absorber theory, if we assume that each particle does not interact with itself and evaluate the field acting on the particle
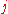at its own position (the point 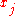) we get:It's clear that if we now add to this the free fields
we obtain
and so
This interpretation avoids the problem of divergent self-energy for a particle giving a reasonably physical interpretation to the equation of Dirac. Moore and Scott showed that the radiation reaction can be alternatively derived using the notion that on average the net dipole moment is zero for a collection of charged particles, thereby avoiding the complications of the absorber theory.
Conclusions
Still this expression of the damping fields is not free of problems, as written in the non-relativistic limit it gives: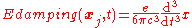which is the Lorentz formulation. Since the third derivative with respect to the time appears here, it is clear that to solve the equation is not sufficient to give just the initial position and velocity of the particle, but the initial acceleration of the particle will also be needed, which makes no sense. This problem is solved by observing that the equation of motion for the particle has to be solved together with the Maxwell equations for the field generated by the particle itself. So instead of giving the initial acceleration one can give the initial field and the boundary condition. This restores the coherence of the physical interpretation of the theory. Still some difficulties may arise when one tries to solve the equation and interpret the solution. It is commonly stated that the Maxwell equations are classical and cannot correctly account for microscopic phenomena such as the behavior of a point-like particle where quantum mechanical effects should appear. However with absorber theory, Wheeler and Feynman were able to create a coherent classical approach to the problem.
When they formulated this paper Wheeler and Feynman were trying to avoid this divergent term. Later however, Feynman would come to state that self-interaction is needed as it correctly accounts, within quantum mechanics, for the Lamb shift. This theory is mentioned in the chapter entitled "Monster Minds" in Feynman's autobiographical work Surely You're Joking, Mr. Feynman!
Surely You're Joking, Mr. Feynman!
"Surely You're Joking, Mr. Feynman!": Adventures of a Curious Character is an edited collection of reminiscences by the Nobel Prize-winning physicist Richard Feynman. The book, released in 1985, covers a variety of instances in Feynman's life...
as well as in Vol. II of the Feynman Lectures on Physics. It led to the formulation of a framework of quantum mechanics using a Lagrangian and action as starting point rather than a Hamiltonian, namely the formulation using Feynman Path integrals
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
which proved useful in Feynman's earliest calculations in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
in general. Both retarded and advanced fields appear respectively as retarded and advanced propagators, and also, in the Feynman propagator and the Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
propagator.
See also
- Action at a distance (physics)Action at a distance (physics)In physics, action at a distance is the interaction of two objects which are separated in space with no known mediator of the interaction. This term was used most often in the context of early theories of gravity and electromagnetism to describe how an object responds to the influence of distant...
- Hoyle–Narlikar theory of gravity
- NonlocalityNonlocalityIn Classical physics, nonlocality is the direct influence of one object on another, distant object. In Quantum mechanics, nonlocality refers to the absence of a local, realist model in agreement with quantum mechanical predictions.Nonlocality may refer to:...
- Symmetry in physicsSymmetry in physicsIn physics, symmetry includes all features of a physical system that exhibit the property of symmetry—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation...
and T-symmetryT-symmetryT Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries... - Wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
and Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations... - PropagatorsPropagatorIn quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
- Relativistic electromagnetismRelativistic electromagnetismRelativistic electromagnetism is a modern teaching strategy for developing electromagnetic field theory from Coulomb’s law and Lorentz transformations. Though Coulomb’s law expresses action at a distance, it is an easily understood electric force principle...
- Quantum electrodynamicsQuantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
- Quantum entanglementQuantum entanglementQuantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
- Transactional interpretationTransactional interpretationThe transactional interpretation of quantum mechanics describes quantum interactions in terms of a standing wave formed by retarded and advanced waves. It was first proposed in 1986 by John G...
- The Feynman Lectures on PhysicsThe Feynman Lectures on PhysicsThe Feynman Lectures on Physics is a 1964 physics textbook by Richard P. Feynman, Robert B. Leighton and Matthew Sands, based upon the lectures given by Feynman to undergraduate students at the California Institute of Technology in 1961–63. It includes lectures on mathematics, electromagnetism,...
(Vol. II - chap. 28) - Two-body problem in general relativity
External links
- J. A. Wheeler and R. P. Feynman, "Interaction with the Absorber as the Mechanism of Radiation" Caltech Library of Authors