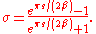N-body problem - AbsoluteAstronomy.com

The -body problem is the problem of predicting the motion of a group of celestial objects that interact with each other gravitationally. Solving this problem has been motivated by the need to understand the motion of the Sun, planets and the visible stars. Its first complete mathematical formulation appeared in Isaac Newton

Isaac Newton

Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...

's Principia (the

-body problem in general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

is considerably more difficult). Since gravity was responsible for the motion of planets and stars, Newton had to express gravitational interactions in terms of differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

s. Newton proved in the Principia that a spherically-symmetric body can be modelled as a point mass.

Informal version of the Newton n-body problem

The physical problem can be informally stated as:

Given only the present positions and velocities of a group of celestial bodies, predict their motions for all future time and deduce them for all past time.

More precisely,

Consider

point masses

, ... ,

in three-dimensional (physical) space. Suppose that the force of attraction experienced between each pair of particles is Newtonian. Then, if the initial positions in space and initial velocities are specified for every particle at some present instant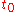

, determine the position of each particle at every future (or past) moment of time.

In mathematical terms, this means to find a global solution of the initial value problem for the differential equations describing the

-body problem.

Mathematical formulation of the n-body problem

The general n-body problem of celestial mechanics is an initial-value problem for ordinary differential equations. Given initial values for the positions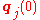

and velocities

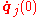of n particles (j = 1,...,n) with

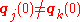for all mutually distinct j and k , find the solution of the second order system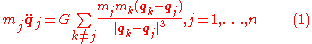

where

are constants representing the masses of n point-masses,

are 3-dimensional vector functions of the time variable t, describing the positions of the point masses, and G is the gravitational constant

Gravitational constant

The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

. This equation is Newton's second law of motion; the left-hand side is the mass times acceleration for the j^th particle, whereas the right-hand side is the sum of the forces on that particle. The forces are assumed here to be gravitation

Gravitation

Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...

al and given by Newton's law of universal gravitation

Newton's law of universal gravitation

Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...

; thus, they are proportional to the masses involved, and vary as the inverse square of the distance between the masses. The power in the denominator is three instead of two to balance the vector difference in the numerator, which is used to specify the direction of the force.

For every solution of the problem, not only applying an isometry

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

or a time shift but also a reversal of time

T-symmetry

T Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries...

(unlike in the case of friction) gives a solution as well.

For n = 2, the problem was completely solved by Johann Bernoulli

Johann Bernoulli

Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...

(see Two-body problem below).

General considerations: solving the -body problem

In the physical literature about the

-body problem (

≥ 3), sometimes reference is made to the impossibility of solving the -body problem. However care must be taken when discussing the 'impossibility' of a solution, as this refers only to the method of first integrals (compare the theorems by Abel

Niels Henrik Abel

Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...

and Galois

Évariste Galois

Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...

about the impossibility of solving algebraic equations of degree five

Quintic equation

In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...

or higher by means of formulas only involving roots).

The -body problem contains 6

variables, since each point particle is represented by three space (displacement) and three momentum components. First integrals (for ordinary differential equations) are functions that remain constant along any given solution of the system, the constant depending on the solution. In other words, integrals provide relations between the variables of the system, so each scalar integral would normally allow the reduction of the system's dimension by one unit. Of course, this reduction can take place only if the integral is an algebraic function not very complicated with respect to its variables. If the integral is transcendent
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...

the reduction cannot be performed.

The

-body problem has 10 independent algebraic integrals

three for the center of mass
three for the linear momentum
three for the angular momentum
one for the energy.

This allows the reduction of variables to 6

− 10. The question at that time was whether there exist other integrals besides these 10. The answer was given in 1887 by H. Bruns.

Theorem (First integrals of the -body problem) The only linearly independent integrals of the -body problem, which are algebraic with respect to 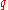, 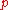and are the 10 described above.

(This theorem was later generalized by Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

). These results however do not imply that there does not exist a general solution of the

-body problem or that the perturbation series (Lindstedt series) diverges. Indeed Sundman provided such a solution by means of convergent series. (See Sundman's theorem for the 3-body problem).

Numerical integration

N-body problems can be solved by numerically integrating the differential equations of motion. Many different ways to do this to varying degrees of accuracy and speed exist.

The simplest integrator is the Euler method, but this is only first order. A second order method is leapfrog integration

Leapfrog integration

Leapfrog integration is a simple method for numerically integrating differential equations of the form\ddot x=F,or equivalently of the form\dot v=F,\;\dot x \equiv v,particularly in the case of a dynamical system of classical mechanics...

, but higher-order integration methods such as the Runge–Kutta methods

Runge–Kutta methods

In numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M.W. Kutta.See the article...

can be employed. Symplectic integrator

Symplectic integrator

In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...

s are often used for n-body problems.

Numerical integration is O(N²), but tree structured algorithms can improve this to O(n log(n)).

Two-body problem

If the common center of mass

Center of mass

In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...

of the two bodies is considered to be at rest, each body travels along a conic section

Conic section

In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

which has a focus

Focus (geometry)

In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...

at the center of mass

Center of mass

of the system (in the case of a hyperbola: the branch at the side of that focus). The two conics will be in the same plane. The type of conic (circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

, ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

, parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

or hyperbola

Hyperbola

In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

) is determined by finding the sum of the combined kinetic energy of two bodies and the potential energy when the bodies are far apart. (This potential energy is always a negative value; energy of rotation of the bodies about their axes is not counted here).

If the sum of the energies is negative, then they both trace out ellipses.
If the sum of both energies is zero, then they both trace out parabolas. As the distance between the bodies tends to infinity, their relative speed tends to zero.
If the sum of both energies is positive, then they both trace out hyperbolas. As the distance between the bodies tends to infinity, their relative speed tends to some positive number.

Note: The fact that a parabolic orbit has zero energy arises from the assumption that the gravitational potential energy goes to zero as the bodies get infinitely far apart. One could assign any value to the potential energy in the state of infinite separation. That state is assumed to have zero potential energy (i.e. 0 joules) by convention.

See also Kepler's first law of planetary motion.

Three-body problem

For n ≥ 3 very little is known about the n-body problem. The case n = 3 was most studied and for many results can be generalized to larger n. Many of the early attempts to understand the 3-body problem were quantitative, aiming at finding explicit solutions for special situations.

In 1687 Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...

published in the Principia the first steps taken in the definition and study of the problem of the movements of three bodies subject to their mutual gravitational attractions. His descriptions were verbal and geometrical, see especially Book 1, Proposition 66 and its corollaries (Newton, 1687 and 1999(transl.), see also Tisserand, 1894).
In 1767 Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

found the collinear periodic orbits, in which three bodies of any masses move such that they oscillate along a rotation line.
In 1772 Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...

discovered some periodic solutions which lie at the vertices of a rotating equilateral triangle that shrinks and expands periodically. Those solutions led to the study of central configurations , for which for some constant k>0 .

Specific solutions to the three-body problem result in chaotic

Chaos theory

Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...

motion with no obvious sign of a repetitious path. A major study of the Earth-Moon-Sun system was undertaken by Charles-Eugène Delaunay

Charles-Eugène Delaunay

Charles-Eugène Delaunay was a French astronomer and mathematician. His lunar motion studies were important in advancing both the theory of planetary motion and mathematics.-Life:...

, who published two volumes on the topic, each of 900 pages in length, in 1860 and 1867. Among many other accomplishments, the work already hints at chaos, and clearly demonstrates the problem of so-called "small denominators" in perturbation theory

Perturbation theory

Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...

.

The restricted three-body problem assumes that the mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

of one of the bodies is negligible; the circular restricted three-body problem

Euler's three-body problem

In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...

is the special case in which two of the bodies are in circular orbits (approximated by the Sun

Sun

The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...

-Earth

Earth

Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...

-Moon

Moon

The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...

system and many others). For a discussion of the case where the negligible body is a satellite of the body of lesser mass, see Hill sphere

Hill sphere

An astronomical body's Hill sphere is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere. That moon would, in turn, have a Hill sphere of its own...

; for binary systems, see Roche lobe

Roche lobe

The Roche lobe is the region of space around a star in a binary system within which orbiting material is gravitationally bound to that star. If the star expands past its Roche lobe, then the material can escape the gravitational pull of the star. If the star is in a binary system then the material...

; for another stable system, see Lagrangian point

Lagrangian point

The Lagrangian points are the five positions in an orbital configuration where a small object affected only by gravity can theoretically be stationary relative to two larger objects...

.

The restricted problem (both circular and elliptical) was worked on extensively by many famous mathematicians and physicists, notably Lagrange

Joseph Louis Lagrange

Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...

in the 18th century and Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

at the end of the 19th century. Poincaré's work on the restricted three-body problem was the foundation of deterministic chaos theory

Chaos theory

. In the circular problem, there exist five equilibrium points. Three are collinear with the masses (in the rotating frame) and are unstable. The remaining two are located on the third vertex of both equilateral triangles of which the two bodies are the first and second vertices. This may be easier to visualize if one considers the more massive body (e.g., Sun

Sun

The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...

) to be "stationary" in space, and the less massive body (e.g., Jupiter

Jupiter

Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...

) to orbit around it, with the equilibrium points maintaining the 60 degree-spacing ahead of and behind the less massive body in its orbit (although in reality neither of the bodies is truly stationary; they both orbit the center of mass of the whole system). For sufficiently small mass ratio of the primaries, these triangular equilibrium points are stable, such that (nearly) massless particles will orbit about these points as they orbit around the larger primary (Sun). The five equilibrium points of the circular problem are known as the Lagrange point

Lagrangian point

The Lagrangian points are the five positions in an orbital configuration where a small object affected only by gravity can theoretically be stationary relative to two larger objects...

The theoretical solution

This is the most elemental way of solving the n-body problem, the theoretical expression. It is often called "The n-body problem by Taylor series

Taylor series

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

", which is an implementation of the Power series solution of differential equations.

We start by defining the differential equations system:

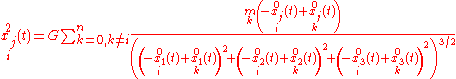
where (in

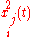) the upper index

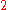indicates the second derivative with respect to time

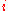represents the number of each body and

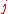the coordinate.

Because

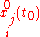and

are given as initial conditions, then every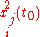

are known. Doing implicit derivation over every

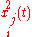results in

which at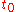

are known because each depends on known

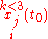precalculated and given constants and then the Taylor series are constructed theoretically in such way, performing this process infinitely.

King Oscar II Prize about the solution for the n-body problem

The problem of finding the general solution of the n-body problem was considered very important and challenging. Indeed in the late 19th century King Oscar II of Sweden

Oscar II of Sweden

Oscar II , baptised Oscar Fredrik was King of Sweden from 1872 until his death and King of Norway from 1872 until 1905. The third son of King Oscar I of Sweden and Josephine of Leuchtenberg, he was a descendant of Gustav I of Sweden through his mother.-Early life:At his birth in Stockholm, Oscar...

, advised by Gösta Mittag-Leffler, established a prize for anyone who could find the solution to the problem. The announcement was quite specific:

Given a system of arbitrarily many mass points that attract each according to Newton's law, under the assumption that no two points ever collide, try to find a representation of the coordinates of each point as a series in a variable that is some known function of time and for all of whose values the series converges uniformly.

In case the problem could not be solved, any other important contribution to classical mechanics would then be considered to be prize-worthy. The prize was finally awarded to Poincaré, even though he did not solve the original problem. (The first version of his contribution even contained a serious error; for details see the article by Diacu). The version finally printed contained many important ideas which led to the development of chaos theory

Chaos theory

. The problem as stated originally was finally solved by Karl Fritiof Sundman for n = 3.

Sundman's theorem for the 3-body problem

In 1912, the Finnish mathematician Karl Fritiof Sundman

Karl Fritiof Sundman

Karl Frithiof Sundman was a Finnish mathematician who used analytic methods to prove the existence of a convergent infinite series solution to the three-body problem in 1906 and 1909....

proved that there exists a series solution in powers of

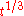for the 3-body problem. This series is convergent for all real t, except initial data which correspond to zero angular momentum. However these initial data are not generic since they have Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

zero.

An important issue in proving this result is the fact that the radius of convergence for this series is determined by the distance to the nearest singularity. Therefore it is necessary to study the possible singularities of the 3-body problems. As it will be briefly discussed in the next section, the only singularities in the 3-body problem are

binary collisions
triple collisions.

Now collisions, whether binary or triple (in fact of arbitrary order), are somehow improbable since it has been shown that they correspond to a set of initial data of measure zero. However there is no criterion known to be put on the initial state in order to avoid collisions for the corresponding solution. So Sundman's strategy consisted of the following steps:

He first was able, using an appropriate change of variables, to continue analytically the solution beyond the binary collision, in a process known as regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...

.
He then proved that triple collisions only occur when the angular momentum L vanishes. By restricting the initial data to 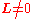he removed all real singularities from the transformed equations for the 3-body problem.
The next step consisted in showing that if then not only can there be no triple collision, but the system is strictly bounded away from a triple collision. This implies, by using the Cauchy existence theorem for differential equations, that there are no complex singularities in a strip (depending on the value of L) in the complex plane centered around the real axis.
The last step is then to find a conformal transformation which maps this strip into the unit disc. For example if 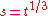(the new variable after the regularization) and if 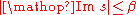then this map is given by

This finishes the proof of Sundman's theorem. Unfortunately the corresponding convergent series converges very slowly. That is, getting the value to any useful precision requires so many terms that his solution is of little practical use.

The global solution of the n-body problem

In order to generalize Sundman's result for the case n>3 (or n=3 and c=0) one has to face two obstacles:

As it has been shown by Siegel, that collisions which involve more than 2 bodies cannot be regularized analytically, hence Sundman's regularization cannot be generalized.
The structure of singularities is more complicated in this case, other types of singularities may occur.

Finally Sundman's result was generalized to the case of n>3 bodies by Q. Wang

Qiudong Wang

Qiudong Wang is an Associate Professor at the Department of Mathematics, the University of Arizona. In 1982 he received a B.S. at Nanjing University and in 1994 a Ph.D. at the University of Cincinnati....

in the 1990s. Since the structure of singularities is more complicated, Wang had to leave out completely the questions of singularities. The central point of his approach is to transform, in an appropriate manner, the equations to a new system, such that the interval of existence for the solutions of this new system is

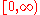Singularities of the n-body problem

There can be two types of singularities of the n-body problem:

collisions of one, two or n particles, but for which q(t) remains finite.

singularities in which a collapse does not occur, but q(t) does not remain finite. The latter ones are called no-collisions singularities. Their existence has been conjectured for n > 3 by Painlevé (see Painlevé's conjecture). Examples of this behavior have been constructed by Xia and Gerver.

External links

Three-Body Problem at Scholarpedia
Scholarpedia
Scholarpedia is an English-language online wiki-based encyclopedia that uses the same MediaWiki software as Wikipedia, but has features more commonly associated with open-access online academic journals....
More detailed information on the three-body problem
Regular Keplerian motions in classical many-body systems
Applet demonstrating chaos in restricted three-body problem
Applets demonstrating many different three-body motions
On the integration of the n-body equations
Java applet simulating Solar System
Java applet simulating a ring of bodies orbiting a large central mass
Java applet simulating dust in the Solar System
Java applet simulating a stable solution to the equi-mass 3-body problem
Java applet simulating choreographies and other interesting n-body solutions
A java applet to simulate the 3-d movement of set of particles under gravitational interaction
Javascript Simulation of our Solar System
programs and informations about many body simulations

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.