
Filter (large eddy simulation)
Encyclopedia
Filtering in the context of large eddy simulation
(LES) is a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations
. Because the principal difficulty in modeling turbulent flows comes from the wide range of length and time scales, this operation makes turbulent flow modeling cheaper by reducing the range of scales that must be calculated. The LES filter operation is low-pass, meaning it filters out the scales associated with high frequencies.
 . The LES filter operation may be spatial, temporal, or both. The filtered field, denoted with a bar, is defined as:
. The LES filter operation may be spatial, temporal, or both. The filtered field, denoted with a bar, is defined as:
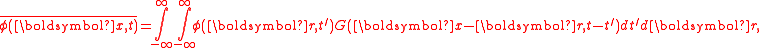
where is a convolution kernel unique to the filter type used. This can be written as a convolution operation:
is a convolution kernel unique to the filter type used. This can be written as a convolution operation:
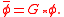
The filter kernel uses cutoff length and time scales, denoted
uses cutoff length and time scales, denoted  and
and 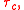 respectively. Scales smaller than these are eliminated from
respectively. Scales smaller than these are eliminated from 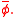 Using this definition, any field
Using this definition, any field  may be split up into a filtered and sub-filtered (denoted with a prime) portion, as
may be split up into a filtered and sub-filtered (denoted with a prime) portion, as
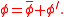
This can also be written as a convolution operation,
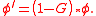
. For a scalar field the Fourier transform
the Fourier transform
of is
is  a function of
a function of  the spatial wave number, and
the spatial wave number, and 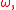 the temporal frequency.
the temporal frequency. 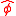 can be filtered by the corresponding Fourier transform
can be filtered by the corresponding Fourier transform
of the filter kernel, denoted
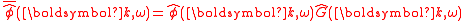
or,
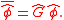
The filter width has an associated cutoff wave number
has an associated cutoff wave number 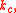 and the temporal filter width
and the temporal filter width 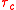 also has an associated cutoff frequency
also has an associated cutoff frequency 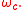 The unfiltered portion of
The unfiltered portion of 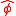 is:
is:
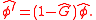
The spectral interpretation of the filtering operation is essential to the filtering operation in large eddy simulation, as the spectra of turbulent flows is central to LES subgrid-scale models, which reconstruct the effect of the sub-filter scales (the highest frequencies). One of the challenges in subgrid modeling is to effectively mimic the cascade of kinetic energy from low to high frequencies. This makes the spectral properties of the implemented LES filter very important to subgrid modeling efforts.
1. Conservation of constants
Large eddy simulation
Large eddy simulation is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and many of the issues unique to LES were first explored by Deardorff...
(LES) is a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
. Because the principal difficulty in modeling turbulent flows comes from the wide range of length and time scales, this operation makes turbulent flow modeling cheaper by reducing the range of scales that must be calculated. The LES filter operation is low-pass, meaning it filters out the scales associated with high frequencies.
Homogeneous filters
Definition in physical space
The low-pass filtering operation used in LES can be applied to a spatial and temporal field, for example . The LES filter operation may be spatial, temporal, or both. The filtered field, denoted with a bar, is defined as:
. The LES filter operation may be spatial, temporal, or both. The filtered field, denoted with a bar, is defined as: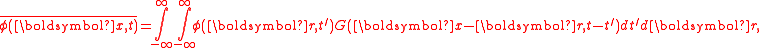
where
 is a convolution kernel unique to the filter type used. This can be written as a convolution operation:
is a convolution kernel unique to the filter type used. This can be written as a convolution operation: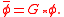
The filter kernel
 uses cutoff length and time scales, denoted
uses cutoff length and time scales, denoted  and
and 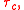 respectively. Scales smaller than these are eliminated from
respectively. Scales smaller than these are eliminated from 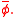 Using this definition, any field
Using this definition, any field  may be split up into a filtered and sub-filtered (denoted with a prime) portion, as
may be split up into a filtered and sub-filtered (denoted with a prime) portion, as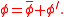
This can also be written as a convolution operation,
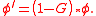
Definition in spectral space
The filtering operation removes scales associated with high frequencies, and the operation can accordingly be interpreted in Fourier spaceFrequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
. For a scalar field
 the Fourier transform
the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of
 is
is  a function of
a function of  the spatial wave number, and
the spatial wave number, and 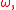 the temporal frequency.
the temporal frequency. 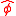 can be filtered by the corresponding Fourier transform
can be filtered by the corresponding Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the filter kernel, denoted

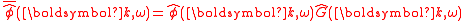
or,
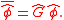
The filter width
 has an associated cutoff wave number
has an associated cutoff wave number 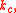 and the temporal filter width
and the temporal filter width 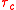 also has an associated cutoff frequency
also has an associated cutoff frequency 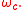 The unfiltered portion of
The unfiltered portion of 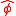 is:
is: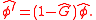
The spectral interpretation of the filtering operation is essential to the filtering operation in large eddy simulation, as the spectra of turbulent flows is central to LES subgrid-scale models, which reconstruct the effect of the sub-filter scales (the highest frequencies). One of the challenges in subgrid modeling is to effectively mimic the cascade of kinetic energy from low to high frequencies. This makes the spectral properties of the implemented LES filter very important to subgrid modeling efforts.
Homogeneous filter properties
Homogeneous LES filters must satisfy the following set of properties when applied to the Navier-Stokes equations.1. Conservation of constants
- The value of a filtered constant must be equal to the constant,
-
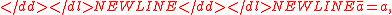
- which implies,
-
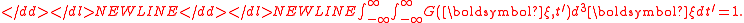
2. Linearity
-

3. Commutation with derivatives
-

- If notation is introduced for operator commutation
 for two arbitrary operators
for two arbitrary operators 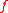 and
and 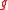 , where
, where
-
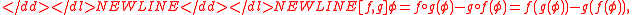
- then this third property can be expressed as
-

Filters satisfying these properties are generally not Reynolds operatorReynolds operatorIn fluid dynamics and invariant theory, a Reynolds operator is a mathematical operator given by averaging something over a group action, that satisfies a set of properties called Reynolds rules...
s, meaning, first:

and second,

Inhomogeneous filters
Implementations of filtering operations for all but the simplest flows are inhomogeneous filter operations. This means that the flow either has non-periodic boundaries, causing problems with certain types of filters, or has a non-constant filter width , or both. This prevents the filter from commuting with derivatives, and the commutation operation leads to several additional error terms:
, or both. This prevents the filter from commuting with derivatives, and the commutation operation leads to several additional error terms:

where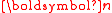 is the vector normal to the surface of the boundary
is the vector normal to the surface of the boundary  and
and 
The two terms both appear due to inhomogeneities. The first is due to the spatial variation in the filter size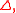 while the second is due to the domain boundary. Similarly, the commutation of the filter
while the second is due to the domain boundary. Similarly, the commutation of the filter  with the temporal derivative leads to an error term resulting from temporal variation in the filter size,
with the temporal derivative leads to an error term resulting from temporal variation in the filter size,

Several filter operations which eliminate or minimize these error terms have been proposed.
Classic large eddy simulation filters
There are three filters ordinarily used for spatial filtering in large eddy simulation. The definition of and
and  and a discussion of important properties, is given.
and a discussion of important properties, is given.
Box filter
The filter kernel in physical space is given by:
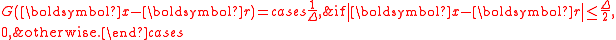
The filter kernel in spectral space is given by:
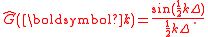
Gaussian filter
The filter kernel in physical space is given by:
The filter kernel in spectral space is given by:

Sharp spectral filter
The filter kernel in physical space is given by:

The filter kernel in spectral space is given by:
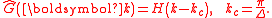
See also
- Computational fluid dynamicsComputational fluid dynamicsComputational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
- Filter (signal processing)Filter (signal processing)In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
- Fluid mechanicsFluid mechanicsFluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
- Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
- Frequency domainFrequency domainIn electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
- Large eddy simulationLarge eddy simulationLarge eddy simulation is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and many of the issues unique to LES were first explored by Deardorff...
- TurbulenceTurbulenceIn fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
- Computational fluid dynamics
- If notation is introduced for operator commutation
-
-

