
Filtered algebra
Encyclopedia
In mathematics
, a filtered algebra is a generalization of the notion of a graded algebra
. Examples appear in many branches of mathematics
, especially in homological algebra
and representation theory
.
A filtered algebra over the field
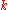 is an algebra
is an algebra
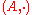 over
over 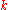 which has an increasing sequence
which has an increasing sequence  of subspaces of
of subspaces of  such that
such that

and that is compatible with the multiplication in the following sense

If is a filtered algebra then the associated graded algebra
is a filtered algebra then the associated graded algebra 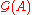 is defined as follows:
is defined as follows:
The multiplication is well defined and endows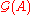 with the structure of a graded algebra, with gradation
with the structure of a graded algebra, with gradation 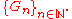 Furthermore if
Furthermore if  is associative then so is
is associative then so is 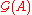 . Also if
. Also if  is unital, such that the unit lies in
is unital, such that the unit lies in 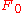 , then
, then 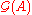 will be unital as well.
will be unital as well.
As algebras and
and  are distinct (with the exception of the trivial case that
are distinct (with the exception of the trivial case that  is graded) but as vector spaces they are isomorphic
is graded) but as vector spaces they are isomorphic
.
graded by ℕ, for example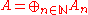 , has a filtration given by
, has a filtration given by  .
.
An example of a filtered algebra is the Clifford algebra
 of a vector space
of a vector space  endowed with a quadratic form
endowed with a quadratic form
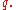 The associated graded algebra is
The associated graded algebra is  , the exterior algebra
, the exterior algebra
of
The symmetric algebra
on the dual of an affine space
is a filtered algebra of polynomials; on a vector space
, one instead obtains a graded algebra.
The universal enveloping algebra
of a Lie algebra
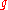 is also naturally filtered. The PBW theorem states that the associated graded algebra is simply
is also naturally filtered. The PBW theorem states that the associated graded algebra is simply  .
.
Scalar differential operator
s on a manifold form a filtered algebra where the filtration is given by the degree of differential operators. The associated graded is the commutative algebra of smooth functions on the cotangent bundle
form a filtered algebra where the filtration is given by the degree of differential operators. The associated graded is the commutative algebra of smooth functions on the cotangent bundle 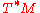 which are polynomial along the fibers of the projection
which are polynomial along the fibers of the projection  .
.
The group algebra
of a group with a length function
is a filtered algebra.
----
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a filtered algebra is a generalization of the notion of a graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
. Examples appear in many branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
.
A filtered algebra over the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
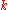 is an algebra
is an algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
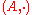 over
over 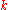 which has an increasing sequence
which has an increasing sequence  of subspaces of
of subspaces of  such that
such that
and that is compatible with the multiplication in the following sense

Associated graded algebra
In general there is the following construction that produces a graded algebra out of a filtered algebra.If
 is a filtered algebra then the associated graded algebra
is a filtered algebra then the associated graded algebra 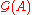 is defined as follows:
is defined as follows: - As a vector space
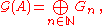
where,
 and
and
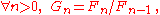
- the multiplication is defined by
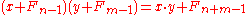
for all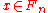 and
and 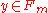 . (More precisely, the multiplication map
. (More precisely, the multiplication map 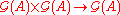 is combined from the maps
is combined from the maps
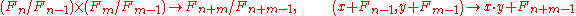
for all and
and  .)
.)
The multiplication is well defined and endows
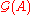 with the structure of a graded algebra, with gradation
with the structure of a graded algebra, with gradation 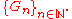 Furthermore if
Furthermore if  is associative then so is
is associative then so is 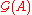 . Also if
. Also if  is unital, such that the unit lies in
is unital, such that the unit lies in 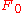 , then
, then 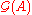 will be unital as well.
will be unital as well.As algebras
 and
and  are distinct (with the exception of the trivial case that
are distinct (with the exception of the trivial case that  is graded) but as vector spaces they are isomorphic
is graded) but as vector spaces they are isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
Examples
Any graded algebraGraded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
graded by ℕ, for example
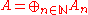 , has a filtration given by
, has a filtration given by  .
.An example of a filtered algebra is the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
 of a vector space
of a vector space  endowed with a quadratic form
endowed with a quadratic formPolarization identity
In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...
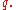 The associated graded algebra is
The associated graded algebra is  , the exterior algebra
, the exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of

The symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
on the dual of an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
is a filtered algebra of polynomials; on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, one instead obtains a graded algebra.
The universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
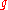 is also naturally filtered. The PBW theorem states that the associated graded algebra is simply
is also naturally filtered. The PBW theorem states that the associated graded algebra is simply  .
.Scalar differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s on a manifold
 form a filtered algebra where the filtration is given by the degree of differential operators. The associated graded is the commutative algebra of smooth functions on the cotangent bundle
form a filtered algebra where the filtration is given by the degree of differential operators. The associated graded is the commutative algebra of smooth functions on the cotangent bundle 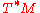 which are polynomial along the fibers of the projection
which are polynomial along the fibers of the projection  .
.The group algebra
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of a group with a length function
Length function
In mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
is a filtered algebra.
See also
- Filtration (mathematics)
- Length functionLength functionIn mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
----

