
Finitely-generated module
Encyclopedia
In mathematics
, a finitely generated module is a module
that has a finite generating set. A finitely generated R-module also may be called a finite R-module or finite over R.
Related concepts include finitely cogenerated modules, finitely presented modules, finitely related modules and coherent modules all of which are defined below. Over a Noetherian ring
the concepts of finitely generated, finitely related, finitely presented and coherent modules all coincide.
A finitely generated module over a field is simply a finite-dimensional vector space
, and a finitely generated module over the integers is simply a finitely generated abelian group
.
there exist a1, a2, ..., an in M such that for all x in M, there exist r1, r2, ..., rn in R with x = r1a1 + r2a2 + ... + rnan.
The set {a1, a2, ..., an} is referred to as a generating set for M in this case.
In the case where the module
M is a vector space
over a field
R, and the generating set is linearly independent, n is well-defined and is referred to as the dimension of M (well-defined means that any linearly independent generating set has n elements: this is the dimension theorem for vector spaces
).
s in countably many variables. R itself is a finitely generated R-module (with {1} as generating set). Consider the submodule K consisting of all those polynomials without constant term. Since every polynomial contains only finitely many variables, the R-module K is not finitely generated.
In general, a module is said to be Noetherian
if every submodule is finitely generated. A finitely generated module over a Noetherian ring is a Noetherian module (and indeed this property characterizes Noetherian rings). This resembles, but is not exactly Hilbert's basis theorem
, which states that the polynomial ring R[X] over a Noetherian ring R is Noetherian. Both facts imply that a finitely generated algebra over a Noetherian ring is again a Noetherian ring.
More generally, an algebra (e.g., ring) that is a finitely-generated module is a finitely-generated algebra. Conversely, if a finitely generated algebra is integral (over the coefficient ring), then it is finitely generated module. (See integral element for more.)
Let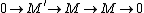 be an exact sequence of modules. Then M is finitely generated if
be an exact sequence of modules. Then M is finitely generated if 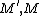 are finitely generated. There are some partial converses to this. If M is finitely generated and M' is finitely presented (which is stronger than finitely generated; see below), then
are finitely generated. There are some partial converses to this. If M is finitely generated and M' is finitely presented (which is stronger than finitely generated; see below), then 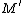 is finitely-generated. Also,
is finitely-generated. Also, 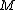 is Noetherian (resp. Artinian) if and only if
is Noetherian (resp. Artinian) if and only if 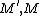 are Noetherian (resp. Artinian).
are Noetherian (resp. Artinian).
Let B be a ring and A its subring such that B is a faithfully flat right A-module. Then a left A-module F is finitely generated (resp. finitely presented) if and only if the B-module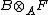 is finitely generated (resp. finitely presented).
is finitely generated (resp. finitely presented).
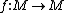 is a surjective R-endomorphism of a finitely generated module M, then f is also injective
is a surjective R-endomorphism of a finitely generated module M, then f is also injective
, and hence is an automorphism
of M. This says simply that M is a Hopfian module. Similarly, an Artinian module
M is coHopfian
: any injective endomorphism f is also a surjective endomorphism.
Any R-module is an inductive limit of finitely generated R-submodules. This is useful for weakening an assumption to the finite case (e.g., the characterization of flatness with the Tor functor
.)
An example of a link between finite generation and integral elements can be found in commutative algebras. To say that a commutative algebra A is a finitely generated ring over R means that there exists a set of elements G={x1...xn} of A such that the smallest subring of A containing G and R is A itself. Because the ring product may be used to combine elements, more than just R combinations of elements of G are generated. For example, a polynomial ring
R[x] is finitely generated by {1,x} as a ring, but not as a module. If A is a commutative algebra (with unity) over R, then the following two statements are equivalent:
From these conditions it is easy to see that being finitely generated is a property preserved by Morita equivalence
. The conditions are also convenient to define a dual
notion of a finitely cogenerated module M. The following conditions are equivalent to a module being finitely cogenerated (f.cog.):
Both f.g. modules and f.cog. modules have interesting relationships to Noetherian and Artinian modules, and the Jacobson radical
J(M) and socle
soc(M) of a module. The following facts illustrate the duality between the two conditions.
For a module M:
Finitely cogenerated modules must have finite uniform dimension. This is easily seen by applying the characterization using the finitely generated essential socle. Somewhat asymmetrically, finitely generated modules do not necessarily have finite uniform dimension. For example, an infinite direct product of nonzero rings is a finitely generated (cyclic!) module over itself, however it clearly contains an infinite direct sum of nonzero submodules. Finitely generated modules do not necessarily have finite co-uniform dimension either: any ring R with unity such that R/J(R) is not a semisimple
ring is a counterexample.
Suppose now there is an epimorphism,
for a module M and free module F.
Over any ring R, coherent modules are finitely presented, and finitely presented modules are both finitely generated and finitely related. For a Noetherian ring
R, all four conditions are actually equivalent.
Some crossover occurs for projective or flat modules. A finitely generated projective module is finitely presented, and a finitely related flat module is projective.
It is true also that the following conditions are equivalent for a ring R:
Although coherence seems like a more cumbersome condition than finitely generated or finitely presented, it is nicer than them since the category
of coherent modules is an abelian category
, while, in general, neither finitely generated nor finitely presented modules form an abelian category.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a finitely generated module is a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
that has a finite generating set. A finitely generated R-module also may be called a finite R-module or finite over R.
Related concepts include finitely cogenerated modules, finitely presented modules, finitely related modules and coherent modules all of which are defined below. Over a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
the concepts of finitely generated, finitely related, finitely presented and coherent modules all coincide.
A finitely generated module over a field is simply a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, and a finitely generated module over the integers is simply a finitely generated abelian group
Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
.
Formal definition
The left R-module M is finitely generated if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exist a1, a2, ..., an in M such that for all x in M, there exist r1, r2, ..., rn in R with x = r1a1 + r2a2 + ... + rnan.
The set {a1, a2, ..., an} is referred to as a generating set for M in this case.
In the case where the module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
R, and the generating set is linearly independent, n is well-defined and is referred to as the dimension of M (well-defined means that any linearly independent generating set has n elements: this is the dimension theorem for vector spaces
Dimension theorem for vector spaces
In mathematics, the dimension theorem for vector spaces states that all bases of a vector space have equally many elements. This number of elements may be finite, or given by an infinite cardinal number, and defines the dimension of the space....
).
Examples
- Let R be an integral domain with K its field of fractions. Then every R-submodule of K is a fractional idealFractional idealIn mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
. If R is Noetherian, every fractional ideal arises in this way. - Finitely generated modules over the ring of integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z coincide with the finitely generated abelian groupFinitely generated abelian groupIn abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
s. These are completely classified by the structure theoremStructure theorem for finitely generated modules over a principal ideal domainIn mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
, taking Z as the principal ideal domain. - Finitely generated modules over division ringDivision ringIn abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s are precisely finite dimensional vector spaces.
Some facts
Every homomorphic image of a finitely generated module is finitely generated. In general, submodules of finitely generated modules need not be finitely generated. As an example, consider the ring R = Z[X1,X2,...] of all polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in countably many variables. R itself is a finitely generated R-module (with {1} as generating set). Consider the submodule K consisting of all those polynomials without constant term. Since every polynomial contains only finitely many variables, the R-module K is not finitely generated.
In general, a module is said to be Noetherian
Noetherian module
In abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
if every submodule is finitely generated. A finitely generated module over a Noetherian ring is a Noetherian module (and indeed this property characterizes Noetherian rings). This resembles, but is not exactly Hilbert's basis theorem
Hilbert's basis theorem
In mathematics, specifically commutative algebra, Hilbert's basis theorem states that every ideal in the ring of multivariate polynomials over a Noetherian ring is finitely generated. This can be translated into algebraic geometry as follows: every algebraic set over a field can be described as the...
, which states that the polynomial ring R[X] over a Noetherian ring R is Noetherian. Both facts imply that a finitely generated algebra over a Noetherian ring is again a Noetherian ring.
More generally, an algebra (e.g., ring) that is a finitely-generated module is a finitely-generated algebra. Conversely, if a finitely generated algebra is integral (over the coefficient ring), then it is finitely generated module. (See integral element for more.)
Let
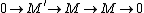 be an exact sequence of modules. Then M is finitely generated if
be an exact sequence of modules. Then M is finitely generated if 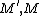 are finitely generated. There are some partial converses to this. If M is finitely generated and M' is finitely presented (which is stronger than finitely generated; see below), then
are finitely generated. There are some partial converses to this. If M is finitely generated and M' is finitely presented (which is stronger than finitely generated; see below), then 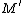 is finitely-generated. Also,
is finitely-generated. Also, 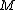 is Noetherian (resp. Artinian) if and only if
is Noetherian (resp. Artinian) if and only if 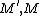 are Noetherian (resp. Artinian).
are Noetherian (resp. Artinian).Let B be a ring and A its subring such that B is a faithfully flat right A-module. Then a left A-module F is finitely generated (resp. finitely presented) if and only if the B-module
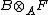 is finitely generated (resp. finitely presented).
is finitely generated (resp. finitely presented).Finitely generated modules over a commutative ring
For finitely generated modules over a commutative ring R, Nakayama's lemma is fundamental. Sometimes, the lemma allows one to prove finite dimensional vector spaces phenomena for finitely generated modules. For example, if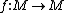 is a surjective R-endomorphism of a finitely generated module M, then f is also injective
is a surjective R-endomorphism of a finitely generated module M, then f is also injectiveInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
, and hence is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of M. This says simply that M is a Hopfian module. Similarly, an Artinian module
Artinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
M is coHopfian
Hopfian object
In the branch of mathematics called category theory, a hopfian object is an object A such that any surjective morphism of A onto A is necessarily an automorphism. The dual notion is that of a cohopfian object, which is an B such that every injective morphism from B into B is necessarily an...
: any injective endomorphism f is also a surjective endomorphism.
Any R-module is an inductive limit of finitely generated R-submodules. This is useful for weakening an assumption to the finite case (e.g., the characterization of flatness with the Tor functor
Tor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
.)
An example of a link between finite generation and integral elements can be found in commutative algebras. To say that a commutative algebra A is a finitely generated ring over R means that there exists a set of elements G={x1...xn} of A such that the smallest subring of A containing G and R is A itself. Because the ring product may be used to combine elements, more than just R combinations of elements of G are generated. For example, a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[x] is finitely generated by {1,x} as a ring, but not as a module. If A is a commutative algebra (with unity) over R, then the following two statements are equivalent:
- A is a finitely generated R module.
- A is both a finitely generated ring over R and an integral extension of R.
Equivalent definitions and finitely cogenerated modules
The following conditions are equivalent to M being finitely generated (f.g.):- For any family of submodules
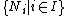 in M, if
in M, if 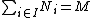 , then
, then 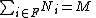 for some finite subset F of I.
for some finite subset F of I.
- For any chain of submodules
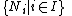 in M, if
in M, if 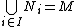 , then
, then 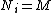 for some i in I.
for some i in I.
- If
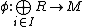 is an epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
is an epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, then the restriction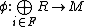 is an epimorphism for some finite subset F of I.
is an epimorphism for some finite subset F of I.
From these conditions it is easy to see that being finitely generated is a property preserved by Morita equivalence
Morita equivalence
In abstract algebra, Morita equivalence is a relationship defined between rings that preserves many ring-theoretic properties. It is named after Japanese mathematician Kiiti Morita who defined equivalence and a similar notion of duality in 1958.- Motivation :...
. The conditions are also convenient to define a dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
notion of a finitely cogenerated module M. The following conditions are equivalent to a module being finitely cogenerated (f.cog.):
- For any family of submodules
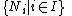 in M, if
in M, if 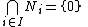 , then
, then 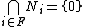 for some finite subset F of I.
for some finite subset F of I.
- For any chain of submodules
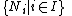 in M, if
in M, if 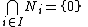 , then
, then 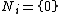 for some i in I.
for some i in I.
- If
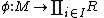 is a monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
is a monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, then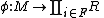 is a monomorphism for some finite subset F of I.
is a monomorphism for some finite subset F of I.
Both f.g. modules and f.cog. modules have interesting relationships to Noetherian and Artinian modules, and the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
J(M) and socle
Socle (mathematics)
-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
soc(M) of a module. The following facts illustrate the duality between the two conditions.
For a module M:
- M is Noetherian if and only if every submodule of N of M is f.g.
- M is Artinian if and only if every quotient module M/N is f.cog.
- M is f.g. if and only if J(M) is a superfluous submodule of M, and M/J(M) is f.g.
- M is f.cog. if and only if soc(M) is an essential submodule of M, and soc(M) is f.g.
- If M is a semisimple moduleSemisimple moduleIn mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
(such as soc(N) for any module N), it is f.g. if and only if f.cog. - If M is f.g. and nonzero, then M has a maximal submodule and any quotient module M/N is f.g.
- If M is f.cog. and nonzero, then M has a minimal submodule, and any submodule N of M is f.cog.
- If N and M/N are f.g. then so is M. The same is true if "f.g." is replaced with "f.cog."
Finitely cogenerated modules must have finite uniform dimension. This is easily seen by applying the characterization using the finitely generated essential socle. Somewhat asymmetrically, finitely generated modules do not necessarily have finite uniform dimension. For example, an infinite direct product of nonzero rings is a finitely generated (cyclic!) module over itself, however it clearly contains an infinite direct sum of nonzero submodules. Finitely generated modules do not necessarily have finite co-uniform dimension either: any ring R with unity such that R/J(R) is not a semisimple
Semisimple
In mathematics, the term semisimple is used in a number of related ways, within different subjects. The common theme is the idea of a decomposition into 'simple' parts, that fit together in the cleanest way...
ring is a counterexample.
Finitely presented, finitely related, and coherent modules
Another formulation is this: a finitely generated module M is one for which there is a epimorphismEpimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
- f : Rk → M.
Suppose now there is an epimorphism,
- φ : F → M.
for a module M and free module F.
- If the kernelKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of φ is finitely generated, then M is called a finitely related module. Since M is isomorphic to F/ker(φ), this basically expresses that M is obtained by taking a free module and introducing finitely many relations within F (the generators of ker(φ)). - If the kernel of φ is finitely generated and F has finite rank (i.e. F=Rk), then M is said to be a finitely presented module. Here, M is specified using finitely many generators (the images of the k generators of F=Rk) and finitely many relations (the generators of ker(φ)).
- A coherent module M is a finitely generated module whose finitely generated submodules are finitely presented.
Over any ring R, coherent modules are finitely presented, and finitely presented modules are both finitely generated and finitely related. For a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
R, all four conditions are actually equivalent.
Some crossover occurs for projective or flat modules. A finitely generated projective module is finitely presented, and a finitely related flat module is projective.
It is true also that the following conditions are equivalent for a ring R:
- R is a right coherent ringCoherent ringIn mathematics, a coherent ring is a ring in which every finitely generated left ideal is finitely presented.Many theorems about finitely generated modules over Noetherian rings can be extended to finitely presented modules over coherent rings....
. - The module RR is a coherent module.
- Every finitely presented right R module is coherent.
Although coherence seems like a more cumbersome condition than finitely generated or finitely presented, it is nicer than them since the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of coherent modules is an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, while, in general, neither finitely generated nor finitely presented modules form an abelian category.
Textbooks
- Bourbaki, NicolasNicolas BourbakiNicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
, Commutative algebra. Chapters 1--7. Translated from the French. Reprint of the 1989 English translation. Elements of Mathematics (Berlin). Springer-Verlag, Berlin, 1998. xxiv+625 pp. ISBN 3-540-64239-0

