Socle of a group

In the context of group theory

Group theory

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...

, the socle of a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 G, denoted Soc(G), is the subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

 generated by the minimal non-trivial normal subgroup

Normal subgroup

In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....

s of G. The socle is a direct product of minimal normal subgroups. As an example, consider the cyclic group

Cyclic group

In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

 Z₁₂ with generator

Generating set of a group

In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...

 u, which has two minimal normal subgroups, one generated by u ⁴ and the other by u ⁶. Thus the socle of Z₁₂ is the group generated by u ⁴ and u ⁶, which is just the group generated by u ².

Socle of a module

In the context of a module

Module (mathematics)

In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...

 M over a ring

Ring (mathematics)

In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

 R, the socle of M is the sum of the minimal nonzero submodules of M. It can be considered as a dual notion

Duality (mathematics)

In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...

 to that of the radical of a module

Radical of a module

In mathematics, in the theory of modules, the radical of a module is a component in the theory of structure and classification. It is a generalization of the Jacobson radical for rings. In many ways, it is the dual notion to that of the socle soc of M.-Definition:Let R be a ring and M a left...

. In set notation,

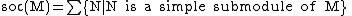
Equivalently,
It is an interesting point that these definitions are dual to those of the radical of a module.

• If M is an Artinian module
  Artinian module
  In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
  
  , soc(M) is itself an essential submodule of M.
• A module is semisimple
  Semisimple module
  In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
  
   if and only if Soc(M) = M. Rings for which soc(M)=M for all M are precisely semisimple rings.
• M is a finitely cogenerated module if and only if soc(M) is finitely generated and rad(M) is an essential submodule of M.
• Since the sum of semisimple modules is semisimple, the socle of a module could also be defined as the unique maximal semi-simple submodule. From the definition of rad(R), it is easy to see that rad(R) annihilates
  Annihilator (ring theory)
  In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
  
   soc(R). If R is a finite dimensional unital algebra
  Algebra
  Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
  
   and M a finitely generated R-module then the socle consists precisely of the elements annihilated by the radical
  Radical of a ring
  In ring theory, a branch of mathematics, a radical of a ring is an ideal of "bad" elements of the ring.The first example of a radical was the nilradical introduced in , based on a suggestion in . In the next few years several other radicals were discovered, of which the most important example is...
  
   of R.

Socle of a Lie algebra

In the context of Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

s, a socle of a symmetric Lie algebra is the eigenspace of its structural automorphism

Automorphism

In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...

 which corresponds to the eigenvalue -1. (A symmetric Lie algebra decomposes into the direct sum

Direct sum of modules

In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...

 of its socle and cosocle

Cosocle

In mathematics, the term cosocle has several related meanings.In group theory, a cosocle of a group G, denoted by Cosoc, is the intersection of all maximal normal subgroups of G....

.)