
Radical of a module
Encyclopedia
In mathematics
, in the theory of module
s, the radical of a module is a component in the theory of structure and classification. It is a generalization of the Jacobson radical
for ring
s. In many ways, it is the dual
notion to that of the socle
soc(M) of M.
and M a left R-module. A submodule N of M is called maximal or cosimple if the quotient M/N is a simple module
. The radical of the module M is the intersection of all maximal submodules of M,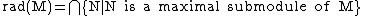
Equivalently,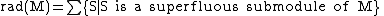
These definitions have direct dual analogues for soc(M).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the theory of module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s, the radical of a module is a component in the theory of structure and classification. It is a generalization of the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
for ring
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
s. In many ways, it is the dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
notion to that of the socle
Socle (mathematics)
-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
soc(M) of M.
Definition
Let R be a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and M a left R-module. A submodule N of M is called maximal or cosimple if the quotient M/N is a simple module
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
. The radical of the module M is the intersection of all maximal submodules of M,
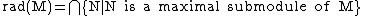
Equivalently,
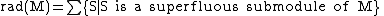
These definitions have direct dual analogues for soc(M).
Properties
- In addition to the fact rad(M) is the sum of superfluous submodules, in a Noetherian moduleNoetherian moduleIn abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
rad(M) itself is a superfluous submodule. - A ring for which rad(M) ={0} for every right R module M is called a right V-ring.
- For any module M, rad(M/rad(M)) is zero.
- M is a finitely generated module if and only if M/rad(M) is finitely generated and rad(M) is a superfluous submodule of M.

