Radical of a ring
Encyclopedia
In ring theory
, a branch of mathematics
, a radical of a ring is an ideal
of "bad" elements of the ring
.
The first example of a radical was the nilradical introduced in , based on a suggestion in . In the next few years several other radicals were discovered, of which the most important example is the Jacobson radical
. The general theory of radicals was defined independently by and .
A radical class (also called radical property or just radical) is a class σ of rings possibly without identities, such that:
(1) the homomorphic image of a ring in σ is also in σ
(2) every ring R contains an ideal S(R) in σ which contains every other ideal in σ
(3) S(R/S(R)) = 0. The ideal S(R) is called the radical, or σ-radical, of R.
The study of such radicals is called torsion theory.
For any class δ of rings, there is a smallest radical class Lδ containing it, called the lower radical of δ. The operator L is called the lower radical operator.
A class of rings is called regular if every non-zero ideal of a ring in the class has a non-zero image in the class. For every regular class δ of rings, there is a largest radical class Uδ, called the upper radical of δ, having zero intersection with δ. The operator U is called the upper radical operator.
A class of rings is called hereditary if every ideal of a ring in the class also belongs to the class.
Let R be any ring, not necessarily commutative. The Jacobson radical of R is the intersection of the annihilators of all simple
right R-modules.
There are several equivalent characterizations of the Jacobson radical, such as:
As with the nilradical, we can extend this definition to arbitrary two-sided ideals I by defining J(I) to be the preimage of J(R/I) under the projection map R→R/I.
If R is commutative, the Jacobson radical always contains the nilradical. If the ring R is a finitely generated Z-algebra, then the nilradical is equal to the Jacobson radical, and more generally: the radical of any ideal I will always be equal to the intersection of all the maximal ideals of R that contain I. This says that R is a Jacobson ring
.
s of the ring R, and the smallest semiprime ideal in R. The Baer radical is the lower radical of the class of nilpotent rings. Also called the "lower nilradical", the "prime radical", and the "Baer-McCoy radical". Every element of the Baer radical is nilpotent
, so it is a nil ideal
.
For commutative rings, this is just the nilradical and closely follows the definition of the radical of an ideal
.
s of a ring R is the upper nilradical Nil*R or Köthe radical and is the unique largest nil ideal of R. Köthe's conjecture asks whether any left nil ideal is in the nilradical.
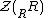. The ideal N of R such that 
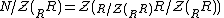is denoted by 
and is called the singular radical or the Goldie torsion of R. The singular radical contains the prime radical (the nilradical in the case of commutative rings) but may properly contain it, even in the commutative case. However, the singular radical of a Noetherian ring
is always nilpotent.
in the theory of groups. If the ring is noetherian
, then the Levitzki radical is itself a nilpotent ideal, and so is the unique largest left, right, or two-sided nilpotent ideal.
The Brown–McCoy radical is studied in much greater generality than associative rings with 1.
is a ring A (possibly non-commutative without identity) such that for every a there is some b with a = aba. The von Neumann regular rings form a radical class. It contains every matrix ring over a division algebra, but contains no nil rings.
s as the sum of all right ideals that are Artinian module
s. The definition is left-right symmetric, and indeed produces a two-sided ideal of the ring. This radical is important in the study of Notherian rings, as outlined in .
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a radical of a ring is an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of "bad" elements of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
The first example of a radical was the nilradical introduced in , based on a suggestion in . In the next few years several other radicals were discovered, of which the most important example is the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
. The general theory of radicals was defined independently by and .
Definitions
In the theory of radicals, rings are usually assumed to be associative, but need not be commutative and need not have an identity element. In particular, every ideal in a ring is also a ring.A radical class (also called radical property or just radical) is a class σ of rings possibly without identities, such that:
(1) the homomorphic image of a ring in σ is also in σ
(2) every ring R contains an ideal S(R) in σ which contains every other ideal in σ
(3) S(R/S(R)) = 0. The ideal S(R) is called the radical, or σ-radical, of R.
The study of such radicals is called torsion theory.
For any class δ of rings, there is a smallest radical class Lδ containing it, called the lower radical of δ. The operator L is called the lower radical operator.
A class of rings is called regular if every non-zero ideal of a ring in the class has a non-zero image in the class. For every regular class δ of rings, there is a largest radical class Uδ, called the upper radical of δ, having zero intersection with δ. The operator U is called the upper radical operator.
A class of rings is called hereditary if every ideal of a ring in the class also belongs to the class.
The Jacobson radical
Let R be any ring, not necessarily commutative. The Jacobson radical of R is the intersection of the annihilators of all simple
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
right R-modules.
There are several equivalent characterizations of the Jacobson radical, such as:
- J(R) is the intersection of the regular maximal right (or left) ideals of R.
- J(R) is the intersection of all the right (or left) primitive ideals of R.
- J(R) is the maximal right (or left) quasi-regular right (resp. left) ideal of R.
As with the nilradical, we can extend this definition to arbitrary two-sided ideals I by defining J(I) to be the preimage of J(R/I) under the projection map R→R/I.
If R is commutative, the Jacobson radical always contains the nilradical. If the ring R is a finitely generated Z-algebra, then the nilradical is equal to the Jacobson radical, and more generally: the radical of any ideal I will always be equal to the intersection of all the maximal ideals of R that contain I. This says that R is a Jacobson ring
Jacobson ring
In mathematics, in the realm of ring theory, a commutative ring with identity is said to be a Hilbert ring or a Jacobson ring if every prime ideal of the ring is an intersection of maximal ideals....
.
The Baer radical
The Baer radical of a rings is the intersection Nil*R of the prime idealPrime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s of the ring R, and the smallest semiprime ideal in R. The Baer radical is the lower radical of the class of nilpotent rings. Also called the "lower nilradical", the "prime radical", and the "Baer-McCoy radical". Every element of the Baer radical is nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
, so it is a nil ideal
Nil ideal
In mathematics, more specifically ring theory, an ideal of a ring is said to be a nil ideal if each of its elements is nilpotent. The nilradical of a commutative ring is an example of a nil ideal; in fact, it is the ideal of the ring maximal with respect to the property of being nil...
.
For commutative rings, this is just the nilradical and closely follows the definition of the radical of an ideal
Radical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
.
The upper nil radical or Köthe radical
The sum of the nil idealNil ideal
In mathematics, more specifically ring theory, an ideal of a ring is said to be a nil ideal if each of its elements is nilpotent. The nilradical of a commutative ring is an example of a nil ideal; in fact, it is the ideal of the ring maximal with respect to the property of being nil...
s of a ring R is the upper nilradical Nil*R or Köthe radical and is the unique largest nil ideal of R. Köthe's conjecture asks whether any left nil ideal is in the nilradical.
Singular radical
An element of a (possibly non-commutative ring) is called left singular if it annihilates an essential left ideal, that is, r is left singular if Ir = 0 for some essential left ideal I. The set of left singular elements of a ring R is a two-sided ideal, called the left singular ideal, and is denoted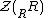. The ideal N of R such that 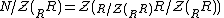is denoted by and is called the singular radical or the Goldie torsion of R. The singular radical contains the prime radical (the nilradical in the case of commutative rings) but may properly contain it, even in the commutative case. However, the singular radical of a Noetherian ringNoetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
is always nilpotent.
The Levitzki radical
The Levitzki radical is defined as the largest locally nilpotent ideal, similarly to the Hirsch–Plotkin radicalHirsch–Plotkin radical
In mathematics, especially in the study of infinite groups, the Hirsch–Plotkin radical is a subgroup describing the normal nilpotent subgroups of the group....
in the theory of groups. If the ring is noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, then the Levitzki radical is itself a nilpotent ideal, and so is the unique largest left, right, or two-sided nilpotent ideal.
The Brown–McCoy radical
The Brown–McCoy radical (called the strong radical in the theory of Banach algebra) can be defined in any of the following ways:- the intersection of the maximal two-sided ideals
- the intersection of all maximal modular ideals
- the upper radical of the class of all simple ringSimple ringIn abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
s with identity
The Brown–McCoy radical is studied in much greater generality than associative rings with 1.
The von Neumann regular radical
A von Neumann regular ringVon Neumann regular ring
In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
is a ring A (possibly non-commutative without identity) such that for every a there is some b with a = aba. The von Neumann regular rings form a radical class. It contains every matrix ring over a division algebra, but contains no nil rings.
The Artinian radical
The Artinian radical is usually defined for two-sided Noetherian ringNoetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s as the sum of all right ideals that are Artinian module
Artinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
s. The definition is left-right symmetric, and indeed produces a two-sided ideal of the ring. This radical is important in the study of Notherian rings, as outlined in .