
Singular submodule
Encyclopedia
In the branches of abstract algebra
known as ring theory
and module theory, each right (resp. left) R module M has a singular submodule consisting of elements whose annihilator
s are essential right (resp. left) ideal
s in R. In set notation it is usually denoted as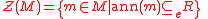 . For general rings,
. For general rings, 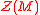 is a good generalization of the torsion submodule t(M) which is most often defined for domain
is a good generalization of the torsion submodule t(M) which is most often defined for domain
s. In the case that R is a commutative domain, .
.
If R is any ring,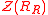 is defined considering R as a right module, and in this case
is defined considering R as a right module, and in this case 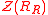 is a twosided ideal of R called the right singular ideal of R. Similarly the left handed analogue
is a twosided ideal of R called the right singular ideal of R. Similarly the left handed analogue  is defined. It is possible for
is defined. It is possible for 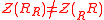 .
.
This article will develop several notions in terms of the singular submodule and singular ideals, including the definition of singular module, nonsingular module and right and left nonsingular ring.
In rings with unity it is always the case that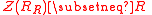 , and so "right singular ring" is not usually defined the same way as singular modules are. Some authors have used "singular ring" to mean "has a nonzero singular ideal", however this usage is not consistent with the usage of the adjectives for modules.
, and so "right singular ring" is not usually defined the same way as singular modules are. Some authors have used "singular ring" to mean "has a nonzero singular ideal", however this usage is not consistent with the usage of the adjectives for modules.
s, and right Rickart rings. This includes right (semi)hereditary ring
s, von Neumann regular ring
s, domain
s, semisimple rings, and Baer ring
s.
For commutative rings, being nonsingular is equivalent to being a reduced ring.
Right nonsingularity has a strong interaction with right self injective rings as well.
Theorem: If R is a right self injective ring, then the following conditions on R are equivalent: right nonsingular, von Neumann regular, right semihereditary, right Rickart, Baer, semiprimitive.
The paper used nonsingular modules to characterize the class of rings whose maximal right ring of quotients have a certain structure.
Theorem: If R is a ring, then is a right full linear ring if and only if R has a nonsingular, faithful, uniform module
is a right full linear ring if and only if R has a nonsingular, faithful, uniform module
. Moreover, is a finite direct product of full linear rings if and only if R has a nonsingular, faithful module with finite uniform dimension.
is a finite direct product of full linear rings if and only if R has a nonsingular, faithful module with finite uniform dimension.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
and module theory, each right (resp. left) R module M has a singular submodule consisting of elements whose annihilator
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
s are essential right (resp. left) ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s in R. In set notation it is usually denoted as
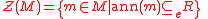 . For general rings,
. For general rings, 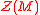 is a good generalization of the torsion submodule t(M) which is most often defined for domain
is a good generalization of the torsion submodule t(M) which is most often defined for domainDomain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
s. In the case that R is a commutative domain,
 .
.If R is any ring,
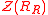 is defined considering R as a right module, and in this case
is defined considering R as a right module, and in this case 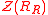 is a twosided ideal of R called the right singular ideal of R. Similarly the left handed analogue
is a twosided ideal of R called the right singular ideal of R. Similarly the left handed analogue  is defined. It is possible for
is defined. It is possible for 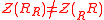 .
.This article will develop several notions in terms of the singular submodule and singular ideals, including the definition of singular module, nonsingular module and right and left nonsingular ring.
Definitions
In the following, M is an R module:- M is called a singular module if
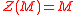 .
. - M is called a nonsingular module if
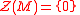 .
. - R is called right nonsingular if
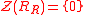 . Using the left singular ideal, a left nonsingular ring is defined similarly, and it is entirely possible for a ring to be right-not-left nonsingular.
. Using the left singular ideal, a left nonsingular ring is defined similarly, and it is entirely possible for a ring to be right-not-left nonsingular.
In rings with unity it is always the case that
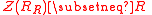 , and so "right singular ring" is not usually defined the same way as singular modules are. Some authors have used "singular ring" to mean "has a nonzero singular ideal", however this usage is not consistent with the usage of the adjectives for modules.
, and so "right singular ring" is not usually defined the same way as singular modules are. Some authors have used "singular ring" to mean "has a nonzero singular ideal", however this usage is not consistent with the usage of the adjectives for modules.Properties
Some general properties of the singular submodule include: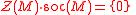 where
where  denotes the socleSocle (mathematics)-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
denotes the socleSocle (mathematics)-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
of M.- If f is a homomorphism of R modules from M to N, then
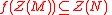 .
. - If N is a submodule of M, then
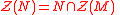 .
. - The properties "singular" and "nonsingular" are Morita invariant propertiesMorita equivalenceIn abstract algebra, Morita equivalence is a relationship defined between rings that preserves many ring-theoretic properties. It is named after Japanese mathematician Kiiti Morita who defined equivalence and a similar notion of duality in 1958.- Motivation :...
. - The singular ideals of a ring contain central nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements of the ring. Consequently the singular ideal of a commutative ring contains the nilradical of the ring. - A general property of the torsion submodule is that
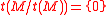 , but this does not necessarily hold for the singular submodule. However if R is a right nonsingular ring, then
, but this does not necessarily hold for the singular submodule. However if R is a right nonsingular ring, then 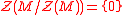 .
. - If N is an essential submodule of M (both right modules) then M/N is singular. If M is a free moduleFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
, or if R is right nonsingular, then the converse is true. - A semisimple moduleSemisimple moduleIn mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
is nonsingular if and only if it is a projective moduleProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
. - If R is a right self-injective ring, then
 , where J(R) is the Jacobson radicalJacobson radicalIn mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
, where J(R) is the Jacobson radicalJacobson radicalIn mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of R.
Examples
Right nonsingular rings are a very broad class, including reduced ringReduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
s, and right Rickart rings. This includes right (semi)hereditary ring
Hereditary ring
In mathematics, especially in the area of abstract algebra known as module theory, a ring R is called hereditary if all submodules of projective modules over R are again projective...
s, von Neumann regular ring
Von Neumann regular ring
In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
s, domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
s, semisimple rings, and Baer ring
Baer ring
In abstract algebra and functional analysis, Baer rings, Baer *-rings, Rickart rings, Rickart *-rings, and AW* algebras are various attempts to give an algebraic analogue of von Neumann algebras, using axioms about annihilators of various sets.Any von Neumann algebra is a Baer *-ring, and much of...
s.
For commutative rings, being nonsingular is equivalent to being a reduced ring.
Important theorems
Johnson's Theorem (due to R. E. Johnson ) contains several important equivalences. For any ring R, the following are equivalent:- R is right nonsingular.
- The injective hullInjective hullIn mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
E(RR) is a nonsingular right R module. - The endomorphism ring
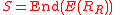 is a semiprimitive ringSemiprimitive ringIn mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
is a semiprimitive ringSemiprimitive ringIn mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
(that is,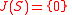 ).
). - The maximal right ring of quotients
 is von Neumann regular.
is von Neumann regular.
Right nonsingularity has a strong interaction with right self injective rings as well.
Theorem: If R is a right self injective ring, then the following conditions on R are equivalent: right nonsingular, von Neumann regular, right semihereditary, right Rickart, Baer, semiprimitive.
The paper used nonsingular modules to characterize the class of rings whose maximal right ring of quotients have a certain structure.
Theorem: If R is a ring, then
 is a right full linear ring if and only if R has a nonsingular, faithful, uniform module
is a right full linear ring if and only if R has a nonsingular, faithful, uniform moduleUniform module
In abstract algebra, a module is called a uniform module if the intersection of any two nonzero submodules is nonzero. This is equivalent to saying that every nonzero submodule of M is an essential submodule...
. Moreover,
 is a finite direct product of full linear rings if and only if R has a nonsingular, faithful module with finite uniform dimension.
is a finite direct product of full linear rings if and only if R has a nonsingular, faithful module with finite uniform dimension.

