
Fisher transformation
Encyclopedia
In statistics
, hypotheses about the value of the population correlation coefficient
ρ between variables X and Y can be tested using the Fisher transformation applied to the sample correlation coefficient
r.
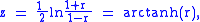
where "ln" is the natural logarithm
function and "arctanh" is the inverse hyperbolic function
.
If (X, Y) has a bivariate normal distribution, and if the (Xi, Yi) pairs used to form r are independent for i = 1, ..., n, then z is approximately normally distributed with mean
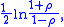
and standard error
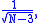
where N is the sample size.
This transformation, and its inverse,

can be used to construct a confidence interval
for ρ.
for r when X and Y follow a bivariate normal distribution. This means that the variance of z is approximately constant for all values of the population correlation coefficient ρ. Without the Fisher transformation, the variance of r grows smaller as |ρ| gets closer to 1. Since the Fisher transformation is approximately the identity function when |r| < 1/2, it is sometimes useful to remember that the variance of r is well approximated by 1/N as long as |ρ| is not too large and N is not too small. This is related to the fact that the asymptotic variance of r is 1 for bivariate normal data.
The behavior of this transform has been extensively studied since Fisher
introduced it in 1915. Fisher himself found the exact distribution of z for data from a bivariate normal distribution in 1921; Gayen, 1951
determined the exact distribution of z for data from a bivariate Type A Edgeworth distribution. Hotelling
in 1953 calculated the Taylor series expressions for the moments of z and several related statistics and Hawkins in 1989 discovered the asymptotic distribution of z for virtually any data.
for bivariate normal observations, it can also be applied to Spearman's rank correlation coefficient
in more general cases. A similar result for the asymptotic distribution
applies, but with a minor adjustment factor: see the latter article for details.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, hypotheses about the value of the population correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
ρ between variables X and Y can be tested using the Fisher transformation applied to the sample correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
r.
Definition
The transformation is defined by: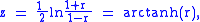
where "ln" is the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
function and "arctanh" is the inverse hyperbolic function
Inverse hyperbolic function
The inverses of the hyperbolic functions are the area hyperbolic functions. The names hint at the fact that they give the area of a sector of the unit hyperbola in the same way that the inverse trigonometric functions give the arc length of a sector on the unit circle...
.
If (X, Y) has a bivariate normal distribution, and if the (Xi, Yi) pairs used to form r are independent for i = 1, ..., n, then z is approximately normally distributed with mean
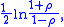
and standard error
Standard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
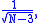
where N is the sample size.
This transformation, and its inverse,

can be used to construct a confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
for ρ.
Discussion
The Fisher transformation is an approximate variance-stabilizing transformationVariance-stabilizing transformation
In applied statistics, a variance-stabilizing transformation is a data transformation that is specifically chosen either to simplify considerations in graphical exploratory data analysis or to allow the application of simple regression-based or analysis of variance techniques.The aim behind the...
for r when X and Y follow a bivariate normal distribution. This means that the variance of z is approximately constant for all values of the population correlation coefficient ρ. Without the Fisher transformation, the variance of r grows smaller as |ρ| gets closer to 1. Since the Fisher transformation is approximately the identity function when |r| < 1/2, it is sometimes useful to remember that the variance of r is well approximated by 1/N as long as |ρ| is not too large and N is not too small. This is related to the fact that the asymptotic variance of r is 1 for bivariate normal data.
The behavior of this transform has been extensively studied since Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
introduced it in 1915. Fisher himself found the exact distribution of z for data from a bivariate normal distribution in 1921; Gayen, 1951
determined the exact distribution of z for data from a bivariate Type A Edgeworth distribution. Hotelling
Harold Hotelling
Harold Hotelling was a mathematical statistician and an influential economic theorist.He was Associate Professor of Mathematics at Stanford University from 1927 until 1931, a member of the faculty of Columbia University from 1931 until 1946, and a Professor of Mathematical Statistics at the...
in 1953 calculated the Taylor series expressions for the moments of z and several related statistics and Hawkins in 1989 discovered the asymptotic distribution of z for virtually any data.
Other uses
While the Fisher transformation is mainly associated with the Pearson product-moment correlation coefficientPearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
for bivariate normal observations, it can also be applied to Spearman's rank correlation coefficient
Spearman's rank correlation coefficient
In statistics, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman and often denoted by the Greek letter \rho or as r_s, is a non-parametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can...
in more general cases. A similar result for the asymptotic distribution
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
applies, but with a minor adjustment factor: see the latter article for details.

