Focused information criterion
Encyclopedia
In statistics
, the focused information criterion (FIC) is a method for selecting the most appropriate model among a set of competitors for a given data set. Unlike most other model selection
strategies, like the Akaike information criterion
(AIC), the Bayesian information criterion (BIC) and the deviance information criterion
(DIC), the FIC does not attempt to assess the overall fit of candidate models but focuses attention directly on the parameter of primary interest with the statistical analysis, say
, for which competing models lead to different estimates, say 
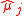for model 
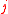. The FIC method consists in first developing an exact or approximate expression for the precision or quality of each estimator
, say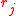
for 
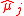, and then use data to estimate these precision measures, say 
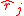. In the end the model with best estimated precision is selected. The FIC methodology was developed by Gerda Claeskens and Nils Lid Hjort
, first in two 2003 discussion articles in Journal of the American Statistical Association
and later on in other papers and in their 2008 book.
The concrete formulae and implementation for FIC depend first of all on the particular interest parameter
, the choice of which does not depend on mathematics but on the scientific and statistical context. Thus the FIC apparatus may be selecting one model as most appropriate for estimating a quantile of a distribution but preferring another model as best for estimating the mean value. Secondly, the FIC formulae depend on the specifics of the models used for the observed data and also on how precision is to be measured. The clearest case is where precision is taken to be mean squared error
(or its square root), say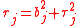
in terms of squared bias
and variance
for the estimator associated with model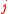
. FIC formulae are then available in a variety of situations, both for handling parametric
, semiparametric and nonparametric
situations, involving separate estimation of squared bias and variance, leading to estimated precision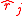
. In the end the FIC selects the model with smallest estimated mean squared error.
Associated with the use of the FIC for selecting a good model is the FIC plot, designed to give a clear and informative picture of all estimates, across all candidate models, and their merit. It displays estimates on the
axis along with FIC scores on the 
axis; thus estimates found to the left in the plot are associated with the better models and those found in the middle and to the right stem from models less or not adequate for the purpose of estimating the focus parameter in question.
Generally speaking, complex models (with many parameters relative to sample size
) tend to lead to estimators with small bias but high variance; more parsimonious models (with fewer parameters) typically yield estimators with larger bias but smaller variance. The FIC method balances the two desiderata of having small bias and small variance in an optimal fashion. The main difficulty lies with the bias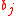
, as it involves the distance from the expected value of the estimator to the true underlying quantity to be estimated, and the true data generating mechanism may lie outside each of the candidate models.
In situations where there is not a unique focus parameter, but rather a family of such, there are versions of average FIC (AFIC or wFIC) that find the best model in terms of suitably weighted performance measures, e.g. when searching for a regression
model to perform particularly well in a portion of the covariate
space.
It is also possible to keep several of the best models on board, ending the statistical analysis with a data-dicated weighted average of the estimators of the best FIC scores, typically giving highest weight to estimators associated with the best FIC scores. Such schemes of model averaging extend the direct FIC selection method.
The FIC methodology applies in particular to selection of variables in different forms of regression analysis
, including the framework of generalised linear models
and the semiparametric proportional hazards models
(i.e. Cox regression).
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the focused information criterion (FIC) is a method for selecting the most appropriate model among a set of competitors for a given data set. Unlike most other model selection
Model selection
Model selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
strategies, like the Akaike information criterion
Akaike information criterion
The Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
(AIC), the Bayesian information criterion (BIC) and the deviance information criterion
Deviance information criterion
The deviance information criterion is a hierarchical modeling generalization of the AIC and BIC . It is particularly useful in Bayesian model selection problems where the posterior distributions of the models have been obtained by Markov chain Monte Carlo simulation...
(DIC), the FIC does not attempt to assess the overall fit of candidate models but focuses attention directly on the parameter of primary interest with the statistical analysis, say
, for which competing models lead to different estimates, say 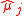for model 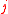. The FIC method consists in first developing an exact or approximate expression for the precision or quality of each estimatorEstimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
, say
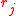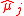for , and then use data to estimate these precision measures, say 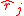. In the end the model with best estimated precision is selected. The FIC methodology was developed by Gerda Claeskens and Nils Lid HjortNils Lid Hjort
Nils Lid Hjort is a Norwegian statistician, and has been a professor of mathematical statistics at the University of Oslo since 1991...
, first in two 2003 discussion articles in Journal of the American Statistical Association
Journal of the American Statistical Association
The Journal of the American Statistical Association is the most prestigious journal published by the American Statistical Association, the main professional body for statisticians in the United States...
and later on in other papers and in their 2008 book.
The concrete formulae and implementation for FIC depend first of all on the particular interest parameter
, the choice of which does not depend on mathematics but on the scientific and statistical context. Thus the FIC apparatus may be selecting one model as most appropriate for estimating a quantile of a distribution but preferring another model as best for estimating the mean value. Secondly, the FIC formulae depend on the specifics of the models used for the observed data and also on how precision is to be measured. The clearest case is where precision is taken to be mean squared errorMean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
(or its square root), say
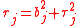in terms of squared biasBias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
for the estimator associated with model
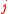. FIC formulae are then available in a variety of situations, both for handling parametricParametric model
In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters...
, semiparametric and nonparametric
Non-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
situations, involving separate estimation of squared bias and variance, leading to estimated precision
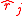. In the end the FIC selects the model with smallest estimated mean squared error.Associated with the use of the FIC for selecting a good model is the FIC plot, designed to give a clear and informative picture of all estimates, across all candidate models, and their merit. It displays estimates on the
axis along with FIC scores on the axis; thus estimates found to the left in the plot are associated with the better models and those found in the middle and to the right stem from models less or not adequate for the purpose of estimating the focus parameter in question.Generally speaking, complex models (with many parameters relative to sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
) tend to lead to estimators with small bias but high variance; more parsimonious models (with fewer parameters) typically yield estimators with larger bias but smaller variance. The FIC method balances the two desiderata of having small bias and small variance in an optimal fashion. The main difficulty lies with the bias
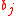, as it involves the distance from the expected value of the estimator to the true underlying quantity to be estimated, and the true data generating mechanism may lie outside each of the candidate models.In situations where there is not a unique focus parameter, but rather a family of such, there are versions of average FIC (AFIC or wFIC) that find the best model in terms of suitably weighted performance measures, e.g. when searching for a regression
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
model to perform particularly well in a portion of the covariate
Covariate
In statistics, a covariate is a variable that is possibly predictive of the outcome under study. A covariate may be of direct interest or it may be a confounding or interacting variable....
space.
It is also possible to keep several of the best models on board, ending the statistical analysis with a data-dicated weighted average of the estimators of the best FIC scores, typically giving highest weight to estimators associated with the best FIC scores. Such schemes of model averaging extend the direct FIC selection method.
The FIC methodology applies in particular to selection of variables in different forms of regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, including the framework of generalised linear models
Generalized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
and the semiparametric proportional hazards models
Proportional hazards models
Proportional hazards models are a class of survival models in statistics. Survival models relate the time that passes before some event occurs to one or more covariates that may be associated with that quantity. In a proportional hazards model, the unique effect of a unit increase in a covariate...
(i.e. Cox regression).
External links
- Interview on frequentist model averaging with Essential Science Indicators
- Webpage for Model Selection and Model Averaging the Claeskens and Hjort book