Deviance information criterion
Encyclopedia
The deviance information criterion (DIC) is a hierarchical modeling generalization of the AIC (Akaike information criterion
) and BIC (Bayesian information criterion
, also known as the Schwarz criterion). It is particularly useful in Bayesian
model selection
problems where the posterior distributions of the model
s have been obtained by Markov chain Monte Carlo
(MCMC) simulation. Like AIC and BIC it is an asymptotic approximation as the sample size becomes large. It is only valid when the posterior distribution is approximately multivariate normal.
Define the deviance as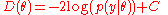
, where 
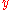are the data, 
are the unknown parameters of the model and 
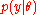is the likelihood function
.
is a constant that cancels out in all calculations that compare different models, and which therefore does not need to be known.
The expectation
is a measure of how well the model fits the data; the larger this is, the worse the fit.
The effective number of parameters of the model is computed as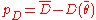
, where 
is the expectation of 
. The larger this is, the easier it is for the model to fit the data.
The deviance information criterion is calculated as
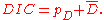
The idea is that models with smaller DIC should be preferred to models with larger DIC. Models are penalized both by the value of
, which favors a good fit, but also (in common with AIC and BIC) by the effective number of parameters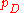 
. Since 
will decrease as the number of parameters in a model increases, the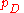 
term compensates for this effect by favoring models with a smaller number of parameters.
The advantage of DIC over other criteria in the case of Bayesian model selection is that the DIC is easily calculated from the samples generated by a Markov chain Monte Carlo simulation. AIC and BIC require calculating the likelihood at its maximum over
, which is not readily available from the MCMC simulation. But to calculate DIC, simply compute 
as the average of 
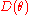over the samples of 
, and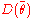 
as the value of 
evaluated at the average of the samples of 
. Then the DIC follows directly from these approximations. Claeskens and Hjort (2008, Ch. 3.5) show that the DIC is large-sample
equivalent to the natural model-robust version of the AIC.
In the derivation of DIC, it assumed that the specified parametric family of probability distributions that generate future observations encompasses the true model. This assumption does not always hold, and it is desirable to consider model assessment procedures in that scenario.
Also, the observed data are used both to construct the posterior distribution and to evaluate the estimated models.
Therefore, DIC tends to select over-fitted models.
Recently, these issues are resolved by Ando (2007), Bayesian predictive information criterion, BPIC.
Akaike information criterion
The Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
) and BIC (Bayesian information criterion
Schwarz criterion
In statistics, the Bayesian information criterion or Schwarz criterion is a criterion for model selection among a finite set of models...
, also known as the Schwarz criterion). It is particularly useful in Bayesian
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
model selection
Model selection
Model selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
problems where the posterior distributions of the model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
s have been obtained by Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
(MCMC) simulation. Like AIC and BIC it is an asymptotic approximation as the sample size becomes large. It is only valid when the posterior distribution is approximately multivariate normal.
Define the deviance as
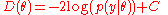, where 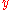are the data, are the unknown parameters of the model and 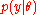is the likelihood functionLikelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
.
is a constant that cancels out in all calculations that compare different models, and which therefore does not need to be known.The expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
is a measure of how well the model fits the data; the larger this is, the worse the fit.The effective number of parameters of the model is computed as
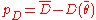, where is the expectation of . The larger this is, the easier it is for the model to fit the data.The deviance information criterion is calculated as
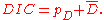
The idea is that models with smaller DIC should be preferred to models with larger DIC. Models are penalized both by the value of
, which favors a good fit, but also (in common with AIC and BIC) by the effective number of parameters 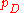. Since will decrease as the number of parameters in a model increases, the 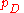term compensates for this effect by favoring models with a smaller number of parameters.The advantage of DIC over other criteria in the case of Bayesian model selection is that the DIC is easily calculated from the samples generated by a Markov chain Monte Carlo simulation. AIC and BIC require calculating the likelihood at its maximum over
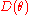, which is not readily available from the MCMC simulation. But to calculate DIC, simply compute as the average of over the samples of , and 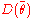as the value of evaluated at the average of the samples of . Then the DIC follows directly from these approximations. Claeskens and Hjort (2008, Ch. 3.5) show that the DIC is large-sampleAsymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
equivalent to the natural model-robust version of the AIC.
In the derivation of DIC, it assumed that the specified parametric family of probability distributions that generate future observations encompasses the true model. This assumption does not always hold, and it is desirable to consider model assessment procedures in that scenario.
Also, the observed data are used both to construct the posterior distribution and to evaluate the estimated models.
Therefore, DIC tends to select over-fitted models.
Recently, these issues are resolved by Ando (2007), Bayesian predictive information criterion, BPIC.
See also
- Akaike information criterionAkaike information criterionThe Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
(AIC) - Bayesian information criterion (BIC)
- Bayesian predictive information criterion (BPIC)
- Focused information criterionFocused information criterionIn statistics, the focused information criterion is a method for selecting the most appropriate model among a set of competitors for a given data set...
(FIC) - Kullback–Leibler divergenceKullback–Leibler divergenceIn probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
- Jensen–Shannon divergenceJensen–Shannon divergenceIn probability theory and statistics, the Jensen–Shannon divergence is a popular method of measuring the similarity between two probability distributions. It is also known as information radius or total divergence to the average. It is based on the Kullback–Leibler divergence, with the notable ...