
Fourier transform on finite groups
Encyclopedia
In mathematics
, the Fourier transform on finite groups is a generalization of the discrete Fourier transform
from cyclic
to arbitrary finite group
s.
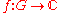
at a representation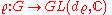 of
of  is
is

So for each representation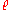 of
of  ,
,  is a
is a  matrix, where
matrix, where 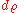 is the degree of
is the degree of 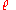 .
.
Let be a complete set of inequivalent irreducible representations of
be a complete set of inequivalent irreducible representations of  . Then,
. Then, 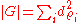 . Then the inverse Fourier transform at an element
. Then the inverse Fourier transform at an element  of
of  is given by
is given by

where is the degree of the representation
is the degree of the representation 
 is defined as
is defined as
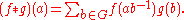
The Fourier transform of a convolution at any representation of
of  is given by
is given by

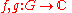 , the Plancherel formula states
, the Plancherel formula states

where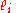 are the irreducible representations of
are the irreducible representations of 
s are all of degree 1 and hence equal to the irreducible characters of the group, Fourier analysis on finite abelian groups is significantly simplified. For instance, the Fourier transform yields a scalar- and not matrix-valued function.
Furthermore, the irreducible characters of a group may be put in one-to-one correspondence with the elements of the group.
Therefore, we may define the Fourier transform for finite abelian groups as

Note that the right-hand side is simply for the inner product on the vector space of functions from
for the inner product on the vector space of functions from  to
to  defined by
defined by

The inverse Fourier transform is then given by

A property that is often useful in probability is that the Fourier transform of the uniform distribution is simply where 0 is the group identity and
where 0 is the group identity and 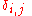 is the Kronecker delta.
is the Kronecker delta.
. A circulant matrix
is a matrix where every column is a cyclic shift of the previous one. Circulant matrices can be diagonalized
quickly using the fast Fourier transform
, and this yields a fast method for solving systems of linear equations with circulant matrices. Similarly, the Fourier transform on arbitrary groups can be used to give fast algorithms for matrices with other symmetries . These algorithms can be used for the construction of numerical methods for solving partial differential equations
that preserve the symmetries of the equations .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fourier transform on finite groups is a generalization of the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
from cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
to arbitrary finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s.
Definitions
The Fourier transform of a function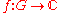
at a representation
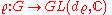 of
of  is
is
So for each representation
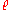 of
of  ,
,  is a
is a  matrix, where
matrix, where 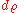 is the degree of
is the degree of 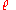 .
.Let
 be a complete set of inequivalent irreducible representations of
be a complete set of inequivalent irreducible representations of  . Then,
. Then, 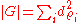 . Then the inverse Fourier transform at an element
. Then the inverse Fourier transform at an element  of
of  is given by
is given by
where
 is the degree of the representation
is the degree of the representation 
Transform of a convolution
The convolution of two functions is defined as
is defined as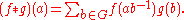
The Fourier transform of a convolution at any representation
 of
of  is given by
is given by
Plancherel formula
For functions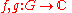 , the Plancherel formula states
, the Plancherel formula states
where
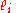 are the irreducible representations of
are the irreducible representations of 
Fourier transform on finite abelian groups
Since the irreducible representations of finite abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s are all of degree 1 and hence equal to the irreducible characters of the group, Fourier analysis on finite abelian groups is significantly simplified. For instance, the Fourier transform yields a scalar- and not matrix-valued function.
Furthermore, the irreducible characters of a group may be put in one-to-one correspondence with the elements of the group.
Therefore, we may define the Fourier transform for finite abelian groups as

Note that the right-hand side is simply
 for the inner product on the vector space of functions from
for the inner product on the vector space of functions from  to
to  defined by
defined by
The inverse Fourier transform is then given by

A property that is often useful in probability is that the Fourier transform of the uniform distribution is simply
 where 0 is the group identity and
where 0 is the group identity and 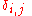 is the Kronecker delta.
is the Kronecker delta.Applications
This generalization of the discrete Fourier transform is used in numerical analysisNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
. A circulant matrix
Circulant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
is a matrix where every column is a cyclic shift of the previous one. Circulant matrices can be diagonalized
Diagonalization
In mathematics, diagonalization may refer to:* Diagonal matrix, which is in a form with nonzero entries only on the main diagonal* Diagonalizable matrix, which can be put into a form with nonzero entries only on the main diagonal...
quickly using the fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
, and this yields a fast method for solving systems of linear equations with circulant matrices. Similarly, the Fourier transform on arbitrary groups can be used to give fast algorithms for matrices with other symmetries . These algorithms can be used for the construction of numerical methods for solving partial differential equations
Numerical partial differential equations
Numerical partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations .Numerical techniques for solving PDEs include the following:...
that preserve the symmetries of the equations .
See also
- Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
- Discrete Fourier transformDiscrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
- Representation theory of finite groupsRepresentation theory of finite groupsIn mathematics, representation theory is a technique for analyzing abstract groups in terms of groups of linear transformations. See the article on group representations for an introduction...
- Character theoryCharacter theoryIn mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....

