Fraysseix-Rosenstiehl's planarity criterion
Encyclopedia
In graph theory
, a branch of mathematics
, Fraysseix–Rosenstiehl's planarity criterion is a characterization of planarity
based on the properties of the trémaux tree
defined by a depth-first search
. It is named after Hubert de Fraysseix and Pierre Rosenstiehl
.
Considering any depth-first search of a graph
G, the edges
encountered when discovering a vertex
for the first time define a DFS-tree T of G. The remaining edges form the cotree. Three types of patterns define two relations on the set of the cotree edges, namely the T-alike and T-opposite relations:
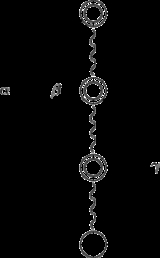
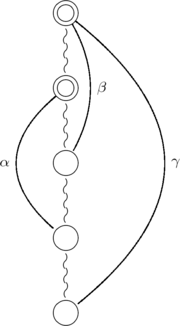
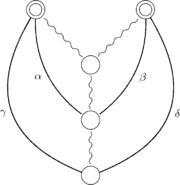
In the following figures, simple circle nodes represent vertices, double circle nodes represent subtrees. Twisted segments represent tree paths and curved arcs represent cotree edges (with label of the edge put near the curved arc). In the first figure,
and 
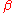are T-alike (it means that their low extremities will be on the same side of the tree in every planar drawing); in the next two figures, they are T-opposite (it means that their low extremities will be on different sides of the tree in every planar drawing).
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Fraysseix–Rosenstiehl's planarity criterion is a characterization of planarity
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
based on the properties of the trémaux tree
Trémaux tree
In graph theory a Trémaux tree of a graph G is a spanning tree of G, rooted at one of its vertices, with the property that every edge in G connects a pair of vertices that are related as ancestor and descendant in the tree...
defined by a depth-first search
Depth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
. It is named after Hubert de Fraysseix and Pierre Rosenstiehl
Pierre Rosenstiehl
Pierre Rosenstiehl is a French mathematician at the École des Hautes Études en Sciences Sociales . He is particularly active in graph theory and recognized for his work on planar graphs and graph drawing...
.
Considering any depth-first search of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
G, the edges
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
encountered when discovering a vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
for the first time define a DFS-tree T of G. The remaining edges form the cotree. Three types of patterns define two relations on the set of the cotree edges, namely the T-alike and T-opposite relations:
In the following figures, simple circle nodes represent vertices, double circle nodes represent subtrees. Twisted segments represent tree paths and curved arcs represent cotree edges (with label of the edge put near the curved arc). In the first figure,
and 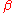are T-alike (it means that their low extremities will be on the same side of the tree in every planar drawing); in the next two figures, they are T-opposite (it means that their low extremities will be on different sides of the tree in every planar drawing). |
 |
 |
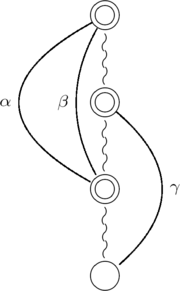- Let G be a graph and let T be a DFS-tree of G. The graph G is planar if and only if there exists a partition of the cotree edges of G into two classes so that any two edges belong to a same class if they are T-alike and any two edges belong to different classes if they are T-opposite.