Frege system
Encyclopedia
In proof complexity
, a Frege system is a propositional proof system
whose proofs are sequences of formulas
derived using a finite set of sound
and implicationally complete inference rules. Frege systems (more often known as Hilbert systems in general proof theory
) are named after Gottlob Frege
.
s built from variables p0, p1, p2, ... using K-connectives. A Frege rule is an inference rule of the form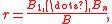
where B1, ..., Bn, B are formulas. If R is a finite set of Frege rules, then F = (K,R) defines a derivation system in the following way. If X is a set of formulas, and A is a formula, then an F-derivation of A from axioms X is a sequence of formulas A1, ..., Am such that Am = A, and every Ak is a member of X, or it is derived from some of the formulas Ai, i < k, by a substitution instance of a rule from R. An F-proof of a formula A is an F-derivation of A from the empty set of axioms (
). F is called a Frege system if
The length (number of lines) in a proof A1, ..., Am is m. The size of the proof is the total number of symbols.
A derivation system F as above is refutationally complete, if for every inconsistent set of formulas X, there is an F-derivation of a fixed contradition from X.
Proof complexity
In computer science, proof complexity is a measure of efficiency of automated theorem proving methods that is based on the size of the proofs they produce. The methods for proving contradiction in propositional logic are the most analyzed...
, a Frege system is a propositional proof system
Propositional proof system
In propositional calculus and proof complexity a propositional proof system , also called a Cook–Reckhow propositional proof system, is system for proving classical propositional tautologies.- Mathematical definition :...
whose proofs are sequences of formulas
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
derived using a finite set of sound
Soundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
and implicationally complete inference rules. Frege systems (more often known as Hilbert systems in general proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
) are named after Gottlob Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
.
Formal definition
Let K be a finite functionally complete set of Boolean connectives, and consider propositional formulaPropositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
s built from variables p0, p1, p2, ... using K-connectives. A Frege rule is an inference rule of the form
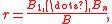
where B1, ..., Bn, B are formulas. If R is a finite set of Frege rules, then F = (K,R) defines a derivation system in the following way. If X is a set of formulas, and A is a formula, then an F-derivation of A from axioms X is a sequence of formulas A1, ..., Am such that Am = A, and every Ak is a member of X, or it is derived from some of the formulas Ai, i < k, by a substitution instance of a rule from R. An F-proof of a formula A is an F-derivation of A from the empty set of axioms (
). F is called a Frege system if
- F is sound: every F-provable formula is a tautology.
- F is implicationally complete: for every formula A and a set of formulas X, if X entails A, then there is an F-derivation of A from X.
The length (number of lines) in a proof A1, ..., Am is m. The size of the proof is the total number of symbols.
A derivation system F as above is refutationally complete, if for every inconsistent set of formulas X, there is an F-derivation of a fixed contradition from X.
Examples
- Frege's propositional calculusFrege's propositional calculusIn mathematical logic Frege's propositional calculus was the first axiomatization of propositional calculus. It was invented by Gottlob Frege, who also invented predicate calculus, in 1879 as part of his second-order predicate calculus .It...
is a Frege system. - There are many examples of sound Frege rules on the Propositional calculusPropositional calculusIn mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
page. - ResolutionResolution (logic)In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation theorem-proving technique for sentences in propositional logic and first-order logic...
is not a Frege system because it only operates on clauses, not on formulas built in an arbitrary way by a functionally complete set of connectives. Moreover, it is not implicationally complete, i.e. we cannot conclude
from 
. However, adding the weakening rule: 
makes it implicationally complete. Resolution is also refutationally complete.
Properties
- Reckhow's theorem (1979) states that all Frege systems are p-equivalent.
- Natural deductionNatural deductionIn logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
and sequent calculusSequent calculusIn proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
(Gentzen system with cut) are also p-equivalent to Frege systems. - There are polynomial-size Frege proofs of the pigeonhole principle (Buss 1987).
- Frege systems are considered to be fairly strong systems. Unlike, say, resolution, there are no known superlinear lower bounds on the number of lines in Frege proofs, and the best known lower bounds on the size of the proofs are quadratic.
- The minimal number of rounds in the prover-adversary game needed to prove a tautology
is proportional to the logarithm of the minimal number of steps in a Frege proof of 
.
Further reading
- MacKay, D. J. (2008). "Information Theory, Inference, and Learning Algorithms"