Frequency partition
Encyclopedia
In graph theory
, a discipline within mathematics
, the frequency partition of a graph (simple graph) is a partition
of its vertices
grouped by their degree.For example, the degree sequence of the left-hand graph below is (3, 3, 3, 2, 2, 1) and its frequency partition is 6 = 3 + 2 + 1. This indicates that it has 3 vertices with some degree, 2 vertices with some other degree, and 1 vertex with a third degree. The degree sequence of the bipartite
graph in the middle below is (3, 2, 2, 2, 2, 2, 1, 1, 1) and its frequency partition is 9 = 5 + 3 + 1. The degree sequence of the right-hand graph below is (3, 3, 3, 3, 3, 3, 2) and its frequency partition is 7 = 6 + 1.
In general, there are many non-isomorphic graphs with a given frequency partition. A graph and its complement
have the same frequency partition. For any partition p = f1 + f2 + ... + fk of an integer p > 1, other than p = 1 + 1 + 1 + ... + 1, there is at least one (connected) simple graph having this partition as its frequency partition.
Frequency partitions of various graph families are completely identifieds; frequency partitions of many families of graphs are not identified.
p = f1 + f2 + ... + fk of an integer p > 1, its graphic degree sequence
is denoted as ((d1)f1,(d2)f2, (d3)f3, ..., (dk) fk) where degrees di's are different and fi ≥ fj for i < j.
Bhat-Nayak et al. (1979) showed that a partition
of p with k parts, k ≤ integral part of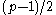
is a frequency partition of a Eulerian graph and conversely.
The graphic degree sequences of the partitions are:
s, Hamiltonian graphs directed graph
s and tournaments
and to k-uniform hypergraph
s. have been characterized.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a discipline within mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the frequency partition of a graph (simple graph) is a partition
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of its vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
grouped by their degree.For example, the degree sequence of the left-hand graph below is (3, 3, 3, 2, 2, 1) and its frequency partition is 6 = 3 + 2 + 1. This indicates that it has 3 vertices with some degree, 2 vertices with some other degree, and 1 vertex with a third degree. The degree sequence of the bipartite
Bipartite
Bipartite means having two parts, or an agreement between two parties. More specifically, it may refer to any of the following:-Mathematics:* 2 * bipartite graph* bipartite cubic, a type of cubic function-Medicine:...
graph in the middle below is (3, 2, 2, 2, 2, 2, 1, 1, 1) and its frequency partition is 9 = 5 + 3 + 1. The degree sequence of the right-hand graph below is (3, 3, 3, 3, 3, 3, 2) and its frequency partition is 7 = 6 + 1.
In general, there are many non-isomorphic graphs with a given frequency partition. A graph and its complement
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
have the same frequency partition. For any partition p = f1 + f2 + ... + fk of an integer p > 1, other than p = 1 + 1 + 1 + ... + 1, there is at least one (connected) simple graph having this partition as its frequency partition.
Frequency partitions of various graph families are completely identifieds; frequency partitions of many families of graphs are not identified.
Frequency partitions of Eulerian graphs
For a frequency partitionPartition
-Computing:* Partition , the division of a database* Disk partitioning, the division of a hard disk drive* Logical partition , a subset of a computer's resources, virtualized as a separate computer-Mathematics:...
p = f1 + f2 + ... + fk of an integer p > 1, its graphic degree sequence
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
is denoted as ((d1)f1,(d2)f2, (d3)f3, ..., (dk) fk) where degrees di's are different and fi ≥ fj for i < j.
Bhat-Nayak et al. (1979) showed that a partition
Partition
-Computing:* Partition , the division of a database* Disk partitioning, the division of a hard disk drive* Logical partition , a subset of a computer's resources, virtualized as a separate computer-Mathematics:...
of p with k parts, k ≤ integral part of
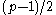is a frequency partition of a Eulerian graph and conversely.The graphic degree sequences of the partitions are:
- For p =
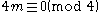, ...(2m + 2)f3,(2m)f1,(2m − 2)f2, ... , example, for 12 = 5 + 4 + 3, the Eulerian degree sequence is 83,65,44.
- For p =
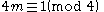, ...(2m + 2)f2,(2m)f1,(2m − 2)f3, ... , example, for 13 = 6 + 4 + 3, the Eulerian degree sequence is 84,66,43.
- For p =
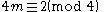, ...(2m + 2)f2,(2m)f1,(2m − 2)f3, ... , example, for 14 = 6 + 5 + 3, the Eulerian degree sequence is 85,66,43.
- For p =
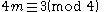, ...(2m + 4)f3,(2m + 2)f1,(2m)f2, ... , example, for 15 = 6 + 5 + 4, the Eulerian degree sequence is 104,86,65.
Frequency partition of trees, Hamiltonian graphs, tournaments and hypegraphs
The frequency partitions of families of graphs such as treeTree
A tree is a perennial woody plant. It is most often defined as a woody plant that has many secondary branches supported clear of the ground on a single main stem or trunk with clear apical dominance. A minimum height specification at maturity is cited by some authors, varying from 3 m to...
s, Hamiltonian graphs directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s and tournaments
Tournament (graph theory)
A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
and to k-uniform hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s. have been characterized.
Unsolved problems in frequency partitions
The frequency partitions of the following families of graphs have not yet been characterized:- Line graphLine graphIn graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
s - Bipartite graphBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s