
Freshman's dream
Encyclopedia
The freshman's dream is a name sometimes given to the error (x + y)n = xn + yn, where n is a real number (usually a positive integer greater than 1). Beginning students commonly make this error in computing the exponential
of a sum of real numbers. When n = 2, it is easy to see why this is incorrect: (x + y)2 can be correctly computed as x2 + 2xy + y2 using distributivity
(or commonly known as the FOIL method). For larger positive integer values of n, the correct result is given by the binomial theorem
.
The name "freshman's dream" also sometimes refers to the theorem that says that for a prime number
p, if x and y are members of a commutative ring
of characteristic
p, then (x + y)p = xp + yp. In this case, the "mistake" actually gives the correct result, due to p dividing all the binomial coefficient
s save the first and the last.
of characteristic
p, then (x + y)p = xp + yp. This can be seen by examining the prime factors of the binomial coefficients: the nth binomial coefficient is

The numerator is p factorial
, which is divisible by p. However, when , neither n! nor is divisible by p since all the terms are less than p and p is prime. Since a binomial coefficient is always an integer, the nth binomial coefficient is divisible by p and hence equal to 0 in the ring. We are left with the zeroth and pth coefficients, which both equal 1, yielding the desired equation.
Thus in characteristic p the freshman's dream is a valid identity. This result demonstrates that exponentiation by p produces an endomorphism
, known as the Frobenius endomorphism
of the ring.
The demand that the characteristic p be a prime number is central to the truth of the freshman's dream. In fact, a related theorem states that a number n is prime if and only if
in the polynomial ring
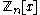 . This theorem is a direct consequence of Fermat's Little Theorem
. This theorem is a direct consequence of Fermat's Little Theorem
and it is a key fact in modern primality testing.
quotes Stephen Kleene
's remark that a knowledge of (a + b)2= a2 + b2 in a field
of characteristic 2 would corrupt freshman students of algebra
. This may be the first connection between "freshman" and binomial expansion in fields of finite characteristic. Since then, authors of undergraduate algebra texts took note of the common error. The first actual attestation of the phrase "freshman's dream" seems to be in Hungerford's
undergraduate algebra textbook (1974), where he quotes McBrien. Alternative terms include "freshman exponentiation", used in Fraleigh (1998). The term "freshman's dream" itself, in non-mathematical contexts, is recorded since the 19th century.
Since the expansion of (x + y)n is correctly given by the binomial theorem
, the freshman's dream is also known as the "Child's Binomial Theorem".
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of a sum of real numbers. When n = 2, it is easy to see why this is incorrect: (x + y)2 can be correctly computed as x2 + 2xy + y2 using distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
(or commonly known as the FOIL method). For larger positive integer values of n, the correct result is given by the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
.
The name "freshman's dream" also sometimes refers to the theorem that says that for a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, if x and y are members of a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
p, then (x + y)p = xp + yp. In this case, the "mistake" actually gives the correct result, due to p dividing all the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s save the first and the last.
Examples
 , but
, but 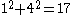 .
.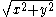 does not generally equal
does not generally equal 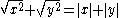 . For example,
. For example, 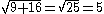 , which does not equal 3+4=7. In this example, the error is being committed with the exponent n = .
, which does not equal 3+4=7. In this example, the error is being committed with the exponent n = .
Prime characteristic
When p is a prime number and x and y are members of a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
p, then (x + y)p = xp + yp. This can be seen by examining the prime factors of the binomial coefficients: the nth binomial coefficient is

The numerator is p factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
, which is divisible by p. However, when , neither n! nor is divisible by p since all the terms are less than p and p is prime. Since a binomial coefficient is always an integer, the nth binomial coefficient is divisible by p and hence equal to 0 in the ring. We are left with the zeroth and pth coefficients, which both equal 1, yielding the desired equation.
Thus in characteristic p the freshman's dream is a valid identity. This result demonstrates that exponentiation by p produces an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
, known as the Frobenius endomorphism
Frobenius endomorphism
In commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
of the ring.
The demand that the characteristic p be a prime number is central to the truth of the freshman's dream. In fact, a related theorem states that a number n is prime if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
in the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
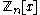 . This theorem is a direct consequence of Fermat's Little Theorem
. This theorem is a direct consequence of Fermat's Little TheoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
and it is a key fact in modern primality testing.
History and alternate names
The history of the term "freshman's dream" is somewhat unclear. In a 1940 article on modular fields, Saunders Mac LaneSaunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
quotes Stephen Kleene
Stephen Cole Kleene
Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
's remark that a knowledge of (a + b)2= a2 + b2 in a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic 2 would corrupt freshman students of algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. This may be the first connection between "freshman" and binomial expansion in fields of finite characteristic. Since then, authors of undergraduate algebra texts took note of the common error. The first actual attestation of the phrase "freshman's dream" seems to be in Hungerford's
Thomas W. Hungerford
Thomas William Hungerford is an American mathematician who works in algebra and mathematics education. He is the author or coauthor of several widely used and widely cited textbooks covering high-school to graduate-level mathematics. From 1963 until 1980 he taught at the University of Washington...
undergraduate algebra textbook (1974), where he quotes McBrien. Alternative terms include "freshman exponentiation", used in Fraleigh (1998). The term "freshman's dream" itself, in non-mathematical contexts, is recorded since the 19th century.
Since the expansion of (x + y)n is correctly given by the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
, the freshman's dream is also known as the "Child's Binomial Theorem".

