
Friendship paradox
Encyclopedia
The friendship paradox is the phenomenon first observed by the sociologist Scott L. Feld in 1991 that most people have fewer friends than their friends have, on average. It can be explained as a form of sampling bias in which people with greater numbers of friends have an increased likelihood of being observed among one's own friends. In contradiction to this, most people believe that they have more friends than their friends do.
The same observation can be applied more generally to social networks defined by other relations than friendship: for instance, most people's sexual partners have (on the average) a greater number of sexual partners than they have.
ical nature, the phenomenon is real, and can be explained as a consequence of the general mathematical properties of social network
s.
Formally, Feld assumes that a social network is represented by an undirected graph , where the set of vertices
corresponds to the people in the social network, and the set of edges corresponds to the friendship relation between pairs of people. That is, he assumes that friendship is a symmetric relation
: if is a friend of , then is a friend of . He models the average number of friends of a person in the social network as the average of the degrees
of the vertices
in the graph. That is, if vertex has edges touching it (representing a person who has friends), then the average number of friends of a random person in the graph is
The average number of friends that a typical friend has can be modeled by choosing, uniformly at random, an edge of the graph (representing a pair of friends) and an endpoint of that edge (one of the friends), and again calculating the degree of the selected endpoint. That is, mathematically, it is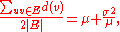
where is the variance
is the variance
of the degrees in the graph. For a graph that has vertices of varying degrees (as is typical for social networks), both and are positive, which implies that the average degree of a friend is strictly greater than the average degree of a random node.
are positive, which implies that the average degree of a friend is strictly greater than the average degree of a random node.
After this analysis, Feld goes on to make some more qualitative assumptions about the statistical correlation between the number of friends that two friends have, based on theories of social networks such as assortative mixing
, and he analyzes what these assumptions imply about the number of people whose friends have more friends than they do. Based on this analysis, he concludes that in real social networks, most people are likely to have fewer friends than the average of their friends' numbers of friends. However, this conclusion is not a mathematical certainty; there exist undirected graphs (such as the graph formed by removing a single edge from a large complete graph
) that are unlikely to arise as social networks but in which most vertices have higher degree than the average of their neighbors' degrees.
. This observation has been used as a way to forecast and slow the course of epidemic
s, by using this random selection process to choose individuals to immunize or monitor for infection while avoiding the need for a complex computation of the centrality of all nodes in the network.
The same observation can be applied more generally to social networks defined by other relations than friendship: for instance, most people's sexual partners have (on the average) a greater number of sexual partners than they have.
Mathematical explanation
In spite of its apparently paradoxParadox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
ical nature, the phenomenon is real, and can be explained as a consequence of the general mathematical properties of social network
Social network
A social network is a social structure made up of individuals called "nodes", which are tied by one or more specific types of interdependency, such as friendship, kinship, common interest, financial exchange, dislike, sexual relationships, or relationships of beliefs, knowledge or prestige.Social...
s.
Formally, Feld assumes that a social network is represented by an undirected graph , where the set of vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
corresponds to the people in the social network, and the set of edges corresponds to the friendship relation between pairs of people. That is, he assumes that friendship is a symmetric relation
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
: if is a friend of , then is a friend of . He models the average number of friends of a person in the social network as the average of the degrees
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
of the vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
in the graph. That is, if vertex has edges touching it (representing a person who has friends), then the average number of friends of a random person in the graph is

The average number of friends that a typical friend has can be modeled by choosing, uniformly at random, an edge of the graph (representing a pair of friends) and an endpoint of that edge (one of the friends), and again calculating the degree of the selected endpoint. That is, mathematically, it is
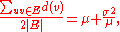
where
 is the variance
is the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the degrees in the graph. For a graph that has vertices of varying degrees (as is typical for social networks), both and
 are positive, which implies that the average degree of a friend is strictly greater than the average degree of a random node.
are positive, which implies that the average degree of a friend is strictly greater than the average degree of a random node.After this analysis, Feld goes on to make some more qualitative assumptions about the statistical correlation between the number of friends that two friends have, based on theories of social networks such as assortative mixing
Assortative mixing
In the study of complex networks, assortative mixing, or assortativity, is a bias in favor of connections between network nodes with similar characteristics. In the specific case of social networks, assortative mixing is also known as homophily...
, and he analyzes what these assumptions imply about the number of people whose friends have more friends than they do. Based on this analysis, he concludes that in real social networks, most people are likely to have fewer friends than the average of their friends' numbers of friends. However, this conclusion is not a mathematical certainty; there exist undirected graphs (such as the graph formed by removing a single edge from a large complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
) that are unlikely to arise as social networks but in which most vertices have higher degree than the average of their neighbors' degrees.
Applications
The analysis of the friendship paradox implies that the friends of randomly selected individuals are likely to have higher than average centralityCentrality
Within graph theory and network analysis, there are various measures of the centrality of a vertex within a graph that determine the relative importance of a vertex within the graph...
. This observation has been used as a way to forecast and slow the course of epidemic
Epidemic
In epidemiology, an epidemic , occurs when new cases of a certain disease, in a given human population, and during a given period, substantially exceed what is expected based on recent experience...
s, by using this random selection process to choose individuals to immunize or monitor for infection while avoiding the need for a complex computation of the centrality of all nodes in the network.

