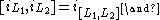Frölicher-Nijenhuis bracket
Encyclopedia
In mathematics
, the Frölicher–Nijenhuis bracket is an extension of the Lie bracket
of vector fields to vector-valued differential forms on a differentiable manifold
. It is useful in the study of connections
, notably the Ehresmann connection
, as well as in the more general study of projections
in the tangent bundle
.
It was introduced by Alfred Frölicher and Albert Nijenhuis
(1956) and is related to the work of Schouten
(1940).
It is related to but not the same as the Nijenhuis–Richardson bracket and the Schouten–Nijenhuis bracket.
of exterior algebra
s of differential form
s on a smooth manifold M. This is a graded algebra
in which forms are graded by degree: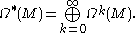
A graded derivation of degree ℓ is a mapping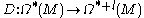
which is linear with respect to constants and satisfies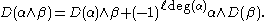
Thus, in particular, the interior product with a vector defines a graded derivation of degree ℓ = −1, whereas the exterior derivative
is a graded derivation of degree ℓ = 1.
The vector space of all derivations of degree ℓ is denoted by DerℓΩ*(M). The direct sum of these spaces is a graded vector space
whose homogeneous components consist of all graded derivations of a given degree; it is denoted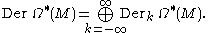
This forms a graded Lie algebra
under the anticommutator of derivations defined on homogeneous derivations D1 and D2 of degrees d1 and d2, respectively, by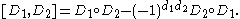
Any vector-valued differential form K in Ωk(M, TM) with values in the tangent bundle
of M defines a graded derivation of degree k − 1, denote by iK, and called the insertion operator. For ω ∈ Ωℓ(M),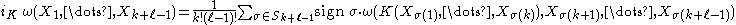
The Nijenhuis–Lie derivative along K ∈ Ωk(M, TM) is defined by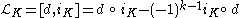
where d is the exterior derivative and iK is the insertion operator.
The Frölicher–Nijenhuis bracket is defined to be the unique vector-valued differential form
such that
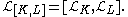
If k = 0, so that K ∈ Ω0(M, TM)
is a vector field, the usual homotopy formula for the Lie derivative is recovered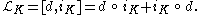
An explicit formula for the Frölicher–Nijenhuis bracket of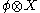
and 
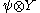(for forms φ and ψ and vector fields X and Y) is given by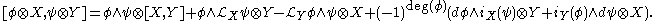
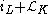
for unique elements K and L of Ω*(M, TM). The Lie bracket of these derivations is given as follows.
With the Frölicher–Nijenhuis bracket it is possible to define the curvature
and cocurvature
of a vector-valued 1-form which is a projection
. This generalizes the concept of the curvature of a connection
.
There is a common generalization of the Schouten–Nijenhuis bracket and the Frölicher–Nijenhuis bracket; for details see the article on the Schouten–Nijenhuis bracket.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Frölicher–Nijenhuis bracket is an extension of the Lie bracket
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of vector fields to vector-valued differential forms on a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
. It is useful in the study of connections
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
, notably the Ehresmann connection
Ehresmann connection
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fibre bundle...
, as well as in the more general study of projections
Projection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
in the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
.
It was introduced by Alfred Frölicher and Albert Nijenhuis
Albert Nijenhuis
Albert Nijenhuis is a Dutch mathematician at the University of Washington and the University of Pennsylvania working on combinatorics and differential geometry, who introduced the Nijenhuis tensor , the Schouten-Nijenhuis bracket , the Frölicher-Nijenhuis bracket , and the Nijenhuis-Richardson...
(1956) and is related to the work of Schouten
Jan Arnoldus Schouten
Jan Arnoldus Schouten was a Dutch mathematician. He was an important contributor to the development of tensor calculus and was one of the founders of the Mathematisch Centrum in Amsterdam....
(1940).
It is related to but not the same as the Nijenhuis–Richardson bracket and the Schouten–Nijenhuis bracket.
Definition
Let Ω*(M) be the sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
s of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on a smooth manifold M. This is a graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
in which forms are graded by degree:
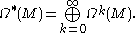
A graded derivation of degree ℓ is a mapping
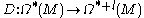
which is linear with respect to constants and satisfies
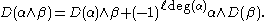
Thus, in particular, the interior product with a vector defines a graded derivation of degree ℓ = −1, whereas the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
is a graded derivation of degree ℓ = 1.
The vector space of all derivations of degree ℓ is denoted by DerℓΩ*(M). The direct sum of these spaces is a graded vector space
Graded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
whose homogeneous components consist of all graded derivations of a given degree; it is denoted
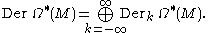
This forms a graded Lie algebra
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
under the anticommutator of derivations defined on homogeneous derivations D1 and D2 of degrees d1 and d2, respectively, by
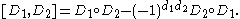
Any vector-valued differential form K in Ωk(M, TM) with values in the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M defines a graded derivation of degree k − 1, denote by iK, and called the insertion operator. For ω ∈ Ωℓ(M),
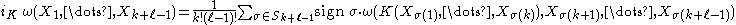
The Nijenhuis–Lie derivative along K ∈ Ωk(M, TM) is defined by
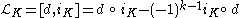
where d is the exterior derivative and iK is the insertion operator.
The Frölicher–Nijenhuis bracket is defined to be the unique vector-valued differential form
such that
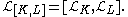
If k = 0, so that K ∈ Ω0(M, TM)
is a vector field, the usual homotopy formula for the Lie derivative is recovered
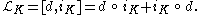
An explicit formula for the Frölicher–Nijenhuis bracket of
and 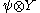(for forms φ and ψ and vector fields X and Y) is given by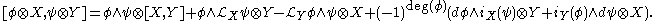Derivations of the ring of forms
Every derivation of Ω*(M) can be written as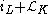for unique elements K and L of Ω*(M, TM). The Lie bracket of these derivations is given as follows.
- The derivations of the form
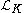form the Lie superalgebra of all derivations commuting with d. The bracket is given by
-
- where the bracket on the right is the Frölicher–Nijenhuis bracket. In particular the Frölicher–Nijenhuis bracket defines a graded Lie algebraGraded Lie algebraIn mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
structure on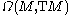
, which extends the Lie bracketLie bracket of vector fieldsIn the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s.- The derivations of the form
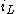form the Lie superalgebra of all derivations vanishing on functions Ω0(M). The bracket is given by
- The derivations of the form
- where the bracket on the right is the Nijenhuis–Richardson bracket.
- The bracket of derivations of different types is given by
- for K in Ωk(M, TM), L in Ωl+1(M, TM).
Applications
The Nijenhuis tensor of an almost complex structure J, is the Frölicher–Nijenhuis bracket of J with itself. An almost complex structure is a complex structure if and only if the Nijenhuis tensor is zero.With the Frölicher–Nijenhuis bracket it is possible to define the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
and cocurvature
Cocurvature
In mathematics in the branch of differential geometry, the cocurvature of a connection on a manifold is the obstruction to the integrability of the vertical bundle.-Definition:...
of a vector-valued 1-form which is a projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
. This generalizes the concept of the curvature of a connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
.
There is a common generalization of the Schouten–Nijenhuis bracket and the Frölicher–Nijenhuis bracket; for details see the article on the Schouten–Nijenhuis bracket.