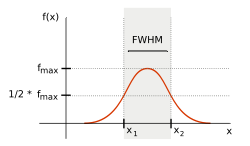
Full width at half maximum (FWHM) is an expression of the extent of a function, given by the difference between the two extreme values of the independent variable

Independent variable

The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...

 at which the dependent variable is equal to half of its maximum value.

FWHM is applied to such phenomena as the duration of pulse

Pulse (signal processing)

In signal processing, the term pulse has the following meanings:#A rapid, transient change in the amplitude of a signal from a baseline value to a higher or lower value, followed by a rapid return to the baseline value....

 waveforms and the spectral width

Spectral width

In telecommunications, spectral width is the wavelength interval over which the magnitude of all spectral components is equal to or greater than a specified fraction of the magnitude of the component having the maximum value....

 of sources used for optical communications

Telecommunication

Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...

 and the resolution of spectrometers.

The term full duration at half maximum (FDHM) is preferred when the independent variable is time

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

.

The convention of "width" meaning "half maximum" is also widely used in signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

 to define bandwidth as "width of frequency range where less than half the signal's power is attenuated", i.e., the power is at least half the maximum. In signal processing terms, this is at most −3 dB

Decibel

The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...

 of attenuation.

When the considered function is the normal distribution of the form


where is the standard deviation

Standard deviation

Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...

 and can be any value (the width of the function does not depend on translation). The relationship between FWHM and the standard deviation is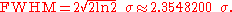


Another important distribution function, related to soliton

Soliton

In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...

s in optics

Optics

Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...

, is the hyperbolic secant:


Any translating element was omitted, since it does not affect the FWHM. For this impulse we have:


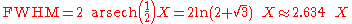
where arsech is the inverse hyperbolic secant

Inverse hyperbolic function

The inverses of the hyperbolic functions are the area hyperbolic functions. The names hint at the fact that they give the area of a sector of the unit hyperbola in the same way that the inverse trigonometric functions give the arc length of a sector on the unit circle...

.