
Gauge symmetry (mathematics)
Encyclopedia
In mathematics, any Lagrangian system
generally admits gauge
symmetries, though it may happen that they are trivial. In
theoretical physics
, the notion of gauge
symmetries depending on parameter functions is a cornerstone of
contemporary field theory.
A gauge symmetry of a Lagrangian
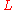 is defined as a differential operator on some
is defined as a differential operator on some
vector bundle
 taking its values in
taking its values in
the linear space of (variational or exact) symmetries of
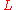 . Therefore, a gauge symmetry of
. Therefore, a gauge symmetry of 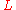
depends on sections of and their partial
and their partial
derivatives. For instance, this is the case of gauge symmetries in
classical field theory
. Yang–Mills gauge
theory and gauge gravitation theory
exemplify classical
field theories with gauge symmetries. Gauge symmetries possess the
following two peculiarities.
(i) Being Lagrangian symmetries, gauge symmetries of a Lagrangian
satisfy first Noether's theorem
, but the
corresponding conserved current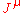 takes a
takes a
particular superpotential form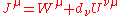 where the first term
where the first term 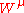
vanishes on solutions of the Euler–Lagrange equations
and the
second one is a boundary term, where is
is
called a superpotential.
(ii) In accordance with second
Noether's theorem
, there is one-to-one correspondence between
the gauge symmetries of a Lagrangian
and the Noether identities
which the Euler–Lagrange operator
satisfies.
Consequently, gauge symmetries characterize the degeneracy of a
Lagrangian system
.
Note that, in quantum field theory
, a generating functional
fail to be invariant under gauge transformations, and gauge
symmetries are replaced with the BRST
symmetries, depending on ghosts and acting both on fields and
ghosts.
Lagrangian system
In mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
generally admits gauge
symmetries, though it may happen that they are trivial. In
theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the notion of gauge
symmetries depending on parameter functions is a cornerstone of
contemporary field theory.
A gauge symmetry of a Lagrangian
Lagrangian system
In mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
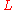 is defined as a differential operator on some
is defined as a differential operator on somevector bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
 taking its values in
taking its values inthe linear space of (variational or exact) symmetries of
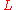 . Therefore, a gauge symmetry of
. Therefore, a gauge symmetry of 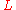
depends on sections of
 and their partial
and their partialderivatives. For instance, this is the case of gauge symmetries in
classical field theory
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
. Yang–Mills gauge
theory and gauge gravitation theory
Gauge gravitation theory
In quantum field theory, gauge gravitation theory is the effort to extend Yang–Mills theory, which provides a universal description of the fundamental interactions, to describe gravity.The first gauge model of gravity was...
exemplify classical
field theories with gauge symmetries. Gauge symmetries possess the
following two peculiarities.
(i) Being Lagrangian symmetries, gauge symmetries of a Lagrangian
Lagrangian system
In mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
satisfy first Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
, but the
corresponding conserved current
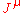 takes a
takes aparticular superpotential form
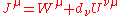 where the first term
where the first term 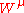
vanishes on solutions of the Euler–Lagrange equations
Lagrangian system
In mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
and the
second one is a boundary term, where
 is
iscalled a superpotential.
(ii) In accordance with second
Noether's theorem
Noether's second theorem
In mathematics, Noether's second theorem relates symmetries of an action functional with a system of differential equations. The action S of a physical system is an integral of a so-called Lagrangian function L, from which the system's behavior can be determined by the principle of least...
, there is one-to-one correspondence between
the gauge symmetries of a Lagrangian
Lagrangian system
In mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
and the Noether identities
Noether identities
In mathematics, Noether identities characterize the degeneracy of a Lagrangian system. Given a Lagrangian system and its Lagrangian L, Noether identities can be defined as a differential operator whose kernel contains a range of the Euler–Lagrange operator of L...
which the Euler–Lagrange operator
Lagrangian system
In mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
satisfies.
Consequently, gauge symmetries characterize the degeneracy of a
Lagrangian system
Lagrangian system
In mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
.
Note that, in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, a generating functional
fail to be invariant under gauge transformations, and gauge
symmetries are replaced with the BRST
symmetries, depending on ghosts and acting both on fields and
ghosts.
See also
- Lagrangian systemLagrangian systemIn mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
- Noether identitiesNoether identitiesIn mathematics, Noether identities characterize the degeneracy of a Lagrangian system. Given a Lagrangian system and its Lagrangian L, Noether identities can be defined as a differential operator whose kernel contains a range of the Euler–Lagrange operator of L...
- Gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
- Gauge symmetry
- Yang–Mills theory
- Gauge gravitation theoryGauge gravitation theoryIn quantum field theory, gauge gravitation theory is the effort to extend Yang–Mills theory, which provides a universal description of the fundamental interactions, to describe gravity.The first gauge model of gravity was...

