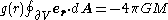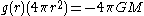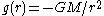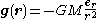Gauss' law for gravity
Encyclopedia
In physics
, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics which is essentially equivalent to Newton's law of universal gravitation
. Although Gauss's law for gravity is physically equivalent to Newton's law, there are many situations where Gauss' law for gravity offers a more convenient and simple way to do a calculation than Newton's law.
The form of Gauss's law for gravity is mathematically similar to Gauss's law
for electrostatics
. Gauss's law for gravity bears the same mathematical relation to Newton's law that Gauss's law for electricity bears to Coulomb's law
. This is because both Newton's law and Coulomb's law describe inverse-square
interaction in a 3-dimensional space. Gauss's law for electricity states:
The electric flux through any closed surface is proportional to the enclosed electric charge
.
And Gauss's law for gravity states:
The gravitational flux through any closed surface is proportional to the enclosed mass
.
The law is expressed in terms of the gravitational field
. The law has two forms, a differential form and an integral form, which are equivalent to each other due to the divergence theorem
.
) is a vector field
– a vector at each point of space (and time). It is defined so that the gravitational force experienced by a particle is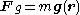
where
where
The left-hand side of this equation is called the flux
of the gravitational field. Note that it is always negative (or zero), and never positive. This can be contrasted with Gauss's law
for electricity, where the flux can be either positive or negative. The difference is because charge can be either positive or negative, while mass can only be positive.
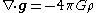
where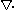
denotes divergence
,
of the universe, ρ is the mass density
at each point.
states: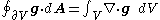
whereg is a continuously differentiable vector field defined on a neighborhood of V,
dV is an infinitesimal piece of the volume V (see volume integral
for more details).
Given also that
we can apply the divergence theorem to the integral form of Gauss's law for gravity, which becomes: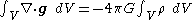
which can be rewritten: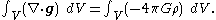
This has to hold simultaneously for every possible volume V; the only way this can happen is if the integrands are equal. Hence we arrive at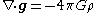
which is the differential form of Gauss's law for gravity.
It is possible to derive the integral form from the differential form using the reverse of this method.
Although the two forms are equivalent, one or the other might be more convenient to use in a particular computation.
, which states that the gravitational field due to a point mass is: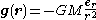
where
In this section, two alternative proofs of this fact are presented. The first proof uses integral calculus and visual notions about field lines, while the second proof uses differential calculus.
Consider a spherical surface of radius r centered at a point-mass of mass M. The total flux of the gravitational field g over a closed surface ∂V, according to Newton's law, is: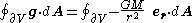
However, the magnitude of the infinitesimal area element dA is just the area of the infinitesimal solid angle
dΩ, given by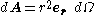
which gives us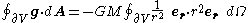
By observing that er·er = 1, and that the integral of unity over a closed surface with respect to the solid angle is the surface area of a unit sphere, 4π, we arrive at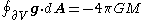
which is the integral form of Gauss' law for gravity, for this special case.
To move to the general case, we use the method of field line
s. The gravitational field can be depicted via field lines, a set of lines or curves that follow the direction of the gravitational field. The magnitude of the field is required to be proportional to the density of field lines. Moreover, it can be shown that the flux
of the field through a surface is proportional to the net number of field lines that pass through the surface (the term "net" means, specifically, the number that pass outward minus the number that pass inward).
Newton's law implies that the field lines will extend directly, radially inward towards the point mass in every direction. Moreover, the special case above shows that if we imagine a series of concentric spheres centered at the point mass, the same number of field lines will pass through each one. So in other words, the field lines all begin at infinity, and go directly inward towards the point mass, ending at the point mass, and coming in uniformly from all directions.
For any finite closed surface (not necessarily spherical) that encloses the point mass, each of the field lines will start at infinity outside the surface, pass through the surface at some point, and end at the point mass inside the surface. Therefore, the flux through the surface is a constant -4πGM, regardless of the shape of the surface, as long as the point mass is inside.
Likewise, for any finite closed surface that does not enclose the point mass, some of the field lines will pass into and then back out of the surface, and some field lines will not touch the surface at all. Regardless, the net flux through the surface is zero.
In every case, this is consistent with Gauss's law. To finish off the proof, we need to consider the case where there is more than one mass (or even infinitely many masses comprising a continuous distribution). The simplest way to handle this case is to say that both Newton's law and Gauss's law obey the superposition principle
, so if Gauss's law is a consequence of Newton's law for a single mass, then it's a consequence of Newton's law for any number of masses. Alternatively, one can note that the net number of field lines that enter a surface equals the number of field lines that end on a mass inside the surface, which is proportional to the total mass inside the surface.
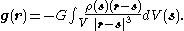
If we take the divergence of both sides of this equation with respect to r, and use the known theorem
where δ(s) is the Dirac delta function
, the result is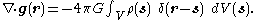
Using the "sifting property" of the Dirac delta function, we arrive at
which is the differential form of Gauss's law for gravity, as desired.
Start with the integral form of Gauss's law:
Apply this law to the situation where the volume V is a sphere of radius r centered on a point-mass M. It's reasonable to expect the gravitational field from a point mass to be spherically symmetric. By making this assumption, g takes the following form:
(i.e., the direction of g is parallel to the direction of r, and the magnitude of g depends only on the magnitude, not direction, of r). Plugging this in, and using the fact that ∂V is a spherical surface with constant r and area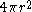
,
which is Newton's law.
), it can be written as the gradient
of a scalar potential
, called the gravitational potential: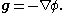
Then the differential form of Gauss's law for gravity becomes Poisson's equation
:
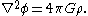
This provides an alternate means of calculating the gravitational potential and gravitational field. Although computing g via Poisson's equation is mathematically equivalent to computing g directly from Gauss's law, one or the other approach may be an easier computation in a given situation.
In radially symmetric systems, the gravitational potential is a function of only one variable (namely,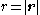
), and Poisson's equation becomes (see Del in cylindrical and spherical coordinates
):
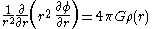
while the gravitational field is: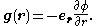
When solving the equation it should be taken into account that in the case of finite densities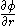
has to be continuous at boundaries (discontinuities of the density), and zero for r = 0.
for more details on how these derivations are done. Three such applications are as follows:
) that for an infinite, flat plate (Bouguer plate) of any finite thickness, the gravitational field outside the plate is perpendicular to the plate, towards it, with magnitude 2πG times the mass per unit area, independent of the distance to the plate (see also gravity anomalies).
More generally, for a mass distribution with the density depending on one Cartesian coordinate z only, gravity for any z is 2πG times (the mass per unit area above z, minus the mass per unit area below z).
In particular, a combination of two equal parallel infinite plates does not produce any gravity inside.
) that the field strength at a distance r from the center is inward with a magnitude of 2G/r times the total mass per unit length at a smaller distance (from the axis), regardless of any masses at a larger distance.
For example, inside an infinite hollow cylinder, the field is zero.
) that the field strength at a distance r from the center is inward with a magnitude of G/r² times only the total mass within a smaller distance than r. All the mass at a greater distance than r from the center can be ignored.
For example, a hollow sphere does not produce any net gravity inside. The gravitational field inside is the same as if the hollow sphere were not there (i.e. the resultant field is that of any masses inside and outside the sphere only).
Although this follows in one or two lines of algebra from Gauss's law for gravity, it took Isaac Newton several pages of cumbersome calculus to derive it directly using his law of gravity; see the article shell theorem
for this direct derivation.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics which is essentially equivalent to Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
. Although Gauss's law for gravity is physically equivalent to Newton's law, there are many situations where Gauss' law for gravity offers a more convenient and simple way to do a calculation than Newton's law.
The form of Gauss's law for gravity is mathematically similar to Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
for electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
. Gauss's law for gravity bears the same mathematical relation to Newton's law that Gauss's law for electricity bears to Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
. This is because both Newton's law and Coulomb's law describe inverse-square
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
interaction in a 3-dimensional space. Gauss's law for electricity states:
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
.
And Gauss's law for gravity states:
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
.
The law is expressed in terms of the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
. The law has two forms, a differential form and an integral form, which are equivalent to each other due to the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
.
Definition of the gravitational field
The gravitational field g (also called gravitational accelerationGravitational acceleration
In physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
) is a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
– a vector at each point of space (and time). It is defined so that the gravitational force experienced by a particle is
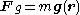
where
- m is the mass of a particle,
- r is the position vector of the particle.
Integral form
The integral form of Gauss's law for gravity states:where
- ∂V is any closed surface,
- dA is a vector, whose magnitude is the area of an infinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
piece of the surface ∂V, and whose direction is the outward-pointing surface normalSurface normalA surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
(see surface integralSurface integralIn mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
for more details), - G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
of the universe, - M is the total mass enclosed within the surface ∂V.
The left-hand side of this equation is called the flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
of the gravitational field. Note that it is always negative (or zero), and never positive. This can be contrasted with Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
for electricity, where the flux can be either positive or negative. The difference is because charge can be either positive or negative, while mass can only be positive.
Differential form
The differential form of Gauss's law for gravity states: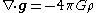where
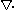denotes divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
,
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
of the universe, ρ is the mass density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
at each point.
Relation to the integral form
The two forms of Gauss's law for gravity are mathematically equivalent. The divergence theoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
states:
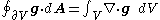
where
Volume integral
In mathematics — in particular, in multivariable calculus — a volume integral refers to an integral over a 3-dimensional domain....
for more details).
Given also that
we can apply the divergence theorem to the integral form of Gauss's law for gravity, which becomes:
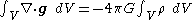
which can be rewritten:
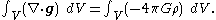
This has to hold simultaneously for every possible volume V; the only way this can happen is if the integrands are equal. Hence we arrive at
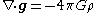
which is the differential form of Gauss's law for gravity.
It is possible to derive the integral form from the differential form using the reverse of this method.
Although the two forms are equivalent, one or the other might be more convenient to use in a particular computation.
Deriving Gauss's law from Newton's law
Gauss's law for gravity can be derived from Newton's law of universal gravitationNewton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
, which states that the gravitational field due to a point mass is:
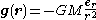
where
- er is the radial unit vector,
- r is the radius, |r|.
- M is the mass of the particle, which is assumed to be a point mass located at the originOrigin (mathematics)In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
.
In this section, two alternative proofs of this fact are presented. The first proof uses integral calculus and visual notions about field lines, while the second proof uses differential calculus.
Special case: Spherical surface centered at a point mass
Consider a spherical surface of radius r centered at a point-mass of mass M. The total flux of the gravitational field g over a closed surface ∂V, according to Newton's law, is:
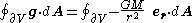
However, the magnitude of the infinitesimal area element dA is just the area of the infinitesimal solid angle
Solid angle
The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
dΩ, given by
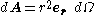
which gives us
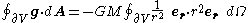
By observing that er·er = 1, and that the integral of unity over a closed surface with respect to the solid angle is the surface area of a unit sphere, 4π, we arrive at
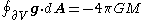
which is the integral form of Gauss' law for gravity, for this special case.
General case
To move to the general case, we use the method of field line
Field line
A field line is a locus that is defined by a vector field and a starting location within the field. Field lines are useful for visualizing vector fields, which are otherwise hard to depict...
s. The gravitational field can be depicted via field lines, a set of lines or curves that follow the direction of the gravitational field. The magnitude of the field is required to be proportional to the density of field lines. Moreover, it can be shown that the flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
of the field through a surface is proportional to the net number of field lines that pass through the surface (the term "net" means, specifically, the number that pass outward minus the number that pass inward).
Newton's law implies that the field lines will extend directly, radially inward towards the point mass in every direction. Moreover, the special case above shows that if we imagine a series of concentric spheres centered at the point mass, the same number of field lines will pass through each one. So in other words, the field lines all begin at infinity, and go directly inward towards the point mass, ending at the point mass, and coming in uniformly from all directions.
For any finite closed surface (not necessarily spherical) that encloses the point mass, each of the field lines will start at infinity outside the surface, pass through the surface at some point, and end at the point mass inside the surface. Therefore, the flux through the surface is a constant -4πGM, regardless of the shape of the surface, as long as the point mass is inside.
Likewise, for any finite closed surface that does not enclose the point mass, some of the field lines will pass into and then back out of the surface, and some field lines will not touch the surface at all. Regardless, the net flux through the surface is zero.
In every case, this is consistent with Gauss's law. To finish off the proof, we need to consider the case where there is more than one mass (or even infinitely many masses comprising a continuous distribution). The simplest way to handle this case is to say that both Newton's law and Gauss's law obey the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
, so if Gauss's law is a consequence of Newton's law for a single mass, then it's a consequence of Newton's law for any number of masses. Alternatively, one can note that the net number of field lines that enter a surface equals the number of field lines that end on a mass inside the surface, which is proportional to the total mass inside the surface.
Proof using differential calculus
An alternative proof derives the differential form of Gauss's law for gravity from Newton's law of universal gravitation. Using the expression from Newton's law, we get the total field at r by using an integral to add up the field at r due to the mass at each other point in space with respect to an s coordinate system, to give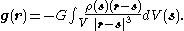If we take the divergence of both sides of this equation with respect to r, and use the known theorem
where δ(s) is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
, the result is
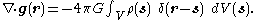
Using the "sifting property" of the Dirac delta function, we arrive at
which is the differential form of Gauss's law for gravity, as desired.
Deriving Newton's law from Gauss's law
Newton's law can be easily proven from Gauss's law, as follows.Start with the integral form of Gauss's law:
Apply this law to the situation where the volume V is a sphere of radius r centered on a point-mass M. It's reasonable to expect the gravitational field from a point mass to be spherically symmetric. By making this assumption, g takes the following form:
(i.e., the direction of g is parallel to the direction of r, and the magnitude of g depends only on the magnitude, not direction, of r). Plugging this in, and using the fact that ∂V is a spherical surface with constant r and area
,
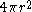which is Newton's law.
Relation to gravitational potential and Poisson's equation
Since the gravitational field has zero curl (equivalently, gravity is a conservative forceConservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
), it can be written as the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar potential
Scalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
, called the gravitational potential:
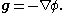
Then the differential form of Gauss's law for gravity becomes Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
:
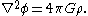
This provides an alternate means of calculating the gravitational potential and gravitational field. Although computing g via Poisson's equation is mathematically equivalent to computing g directly from Gauss's law, one or the other approach may be an easier computation in a given situation.
In radially symmetric systems, the gravitational potential is a function of only one variable (namely,
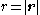), and Poisson's equation becomes (see Del in cylindrical and spherical coordinatesDel in cylindrical and spherical coordinates
This is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.- Note :* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in...
):
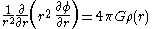
while the gravitational field is:
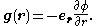
When solving the equation it should be taken into account that in the case of finite densities
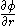has to be continuous at boundaries (discontinuities of the density), and zero for r = 0.Applications
Gauss's law can be used to easily derive the gravitational field in certain cases where a direct application of Newton's law would be more difficult (but not impossible). See the article Gaussian surfaceGaussian surface
A Gaussian surface is a closed surface in three dimensional space through which the flux of an electromagnetic field is calculated. It is an arbitrary closed surface S=\partial V used in conjunction with Gauss's law in order to calculate the total enclosed electric charge by performing a surface...
for more details on how these derivations are done. Three such applications are as follows:
Bouguer plate
We can conclude (by using a "Gaussian pillbox"Gaussian surface
A Gaussian surface is a closed surface in three dimensional space through which the flux of an electromagnetic field is calculated. It is an arbitrary closed surface S=\partial V used in conjunction with Gauss's law in order to calculate the total enclosed electric charge by performing a surface...
) that for an infinite, flat plate (Bouguer plate) of any finite thickness, the gravitational field outside the plate is perpendicular to the plate, towards it, with magnitude 2πG times the mass per unit area, independent of the distance to the plate (see also gravity anomalies).
More generally, for a mass distribution with the density depending on one Cartesian coordinate z only, gravity for any z is 2πG times (the mass per unit area above z, minus the mass per unit area below z).
In particular, a combination of two equal parallel infinite plates does not produce any gravity inside.
Cylindrically symmetric mass distribution
In the case of an infinite cylindrically symmetric mass distribution we can conclude (by using a cylindrical Gaussian surfaceGaussian surface
A Gaussian surface is a closed surface in three dimensional space through which the flux of an electromagnetic field is calculated. It is an arbitrary closed surface S=\partial V used in conjunction with Gauss's law in order to calculate the total enclosed electric charge by performing a surface...
) that the field strength at a distance r from the center is inward with a magnitude of 2G/r times the total mass per unit length at a smaller distance (from the axis), regardless of any masses at a larger distance.
For example, inside an infinite hollow cylinder, the field is zero.
Spherically symmetric mass distribution
In the case of a spherically symmetric mass distribution we can conclude (by using a spherical Gaussian surfaceGaussian surface
A Gaussian surface is a closed surface in three dimensional space through which the flux of an electromagnetic field is calculated. It is an arbitrary closed surface S=\partial V used in conjunction with Gauss's law in order to calculate the total enclosed electric charge by performing a surface...
) that the field strength at a distance r from the center is inward with a magnitude of G/r² times only the total mass within a smaller distance than r. All the mass at a greater distance than r from the center can be ignored.
For example, a hollow sphere does not produce any net gravity inside. The gravitational field inside is the same as if the hollow sphere were not there (i.e. the resultant field is that of any masses inside and outside the sphere only).
Although this follows in one or two lines of algebra from Gauss's law for gravity, it took Isaac Newton several pages of cumbersome calculus to derive it directly using his law of gravity; see the article shell theorem
Shell theorem
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
for this direct derivation.