Geometric spanner
Encyclopedia
A geometric spanner or a k-spanner graph or a k-spanner was initially introduced as a weighted graph over a set of points as its vertices which for every pair of vertices has a path between them of weight at most k times the spatial distance between these points for a fixed k. The parameter k is called the stretch factor or dilation factor of the spanner.
In computational geometry
, the concept was first discussed by L.P. Chew in 1986, although the term "spanner" was not used in the original paper.
The notion of graph spanners has been known in graph theory
: k-spanners are spanning subgraphs of graphs with similar dilation property, where distances between graph vertices are defined in graph-theoretical terms. Therefore geometric spanners are graph spanners of complete graph
s embedded in the plane
with edge weights equal to the distances between the embedded vertices in the corresponding metric.
Spanners may be used in computational geometry
for solving some proximity problems
. They have also found applications in other areas, such as in motion planning
, in telecommunication networks: network reliability, optimization of roaming
in mobile networks, etc.
of this pointset such that for any two points there is a path along the edges of the triangulation with length at most
the Euclidean distance
between the two points. The result was applied in motion planning for finding reasonable approximations of shortest paths among obstacles.
The best upper bound known for the Euclidean Delaunay triangulation
is that it is a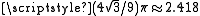
-spanner for its vertices.
The lower bound has been increased from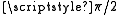
to just over that, to 1.5846.
Finding a spanner in the Euclidean plane with minimal dilation over n points with at most m edges is known to be NP-hard
.
In computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, the concept was first discussed by L.P. Chew in 1986, although the term "spanner" was not used in the original paper.
The notion of graph spanners has been known in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
: k-spanners are spanning subgraphs of graphs with similar dilation property, where distances between graph vertices are defined in graph-theoretical terms. Therefore geometric spanners are graph spanners of complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
s embedded in the plane
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
with edge weights equal to the distances between the embedded vertices in the corresponding metric.
Spanners may be used in computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
for solving some proximity problems
Proximity problems
Proximity problems is a class of problems in computational geometry which involve estimation of distances between geometric objects.A subset of these problems stated in terms of points only are sometimes referred to as closest point problems, although the term "closest point problem" is also used...
. They have also found applications in other areas, such as in motion planning
Motion planning
Motion planning is a term used in robotics for the process of detailing a task into discrete motions....
, in telecommunication networks: network reliability, optimization of roaming
Roaming
In wireless telecommunications, roaming is a general term referring to the extension of connectivity service in a location that is different from the home location where the service was registered. Roaming ensures that the wireless device is kept connected to the network, without losing the...
in mobile networks, etc.
Research
Chew's main result was that for a set of points in the plane there is a triangulationTriangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
of this pointset such that for any two points there is a path along the edges of the triangulation with length at most
the Euclidean distanceEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between the two points. The result was applied in motion planning for finding reasonable approximations of shortest paths among obstacles.
The best upper bound known for the Euclidean Delaunay triangulation
Delaunay triangulation
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
is that it is a
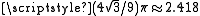-spanner for its vertices.The lower bound has been increased from
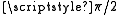to just over that, to 1.5846.Finding a spanner in the Euclidean plane with minimal dilation over n points with at most m edges is known to be NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
.