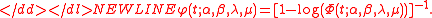Geometric stable distribution
Encyclopedia
A geometric stable distribution or geo-stable distribution is a type of leptokurtic probability distribution
. The geometric stable distribution may be symmetric or asymmetric. A symmetric geometric stable distribution is also referred to as a Linnik distribution. The Laplace distribution is a special case of the geometric stable distribution and of a Linnik distribution. The Mittag–Leffler distribution is also a special case of a geometric stable distribution.
The geometric stable distribution has applications in finance theory.
and cumulative distribution function
have no closed form solution. But a geometric stable distribution can be defined by its characteristic function
, which has the form:
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. The geometric stable distribution may be symmetric or asymmetric. A symmetric geometric stable distribution is also referred to as a Linnik distribution. The Laplace distribution is a special case of the geometric stable distribution and of a Linnik distribution. The Mittag–Leffler distribution is also a special case of a geometric stable distribution.
The geometric stable distribution has applications in finance theory.
Characteristics
For most geometric stable distributions, the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
and cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
have no closed form solution. But a geometric stable distribution can be defined by its characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
, which has the form:
-

where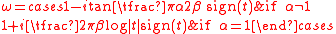
 , which must be greater than 0 and less than or equal to 2, is the shape parameter or index of stability, which determines how heavy the tails are. Lower
, which must be greater than 0 and less than or equal to 2, is the shape parameter or index of stability, which determines how heavy the tails are. Lower  corresponds to heavier tails.
corresponds to heavier tails.
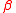 , which must be greater than or equal to −1 and less than or equal to 1, is the skewness parameter. When
, which must be greater than or equal to −1 and less than or equal to 1, is the skewness parameter. When 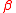 is negative the distribution is skewed to the left and when
is negative the distribution is skewed to the left and when 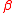 is positive the distribution is skewed to the right. When
is positive the distribution is skewed to the right. When 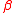 is zero the distribution is symmetric, and the characteristic function reduces to:
is zero the distribution is symmetric, and the characteristic function reduces to:
-
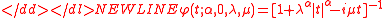
The symmetric geometric stable distribution with is also referred to as a Linnik distribution. A completely skewed geometric stable distribution, that is with
is also referred to as a Linnik distribution. A completely skewed geometric stable distribution, that is with  ,
,  , with
, with  is also referred to as a Mittag–Leffler distribution. Although
is also referred to as a Mittag–Leffler distribution. Although 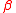 determines the skewness of the distribution, it should not be confused with the typical skewness coefficientSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
determines the skewness of the distribution, it should not be confused with the typical skewness coefficientSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
or 3rd standardized moment, which in most circumstances is undefined for a geometric stable distribution.
 is the scale parameterScale parameterIn probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
is the scale parameterScale parameterIn probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
and is the location parameter.
is the location parameter.
When = 2,
= 2, 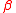 = 0 and
= 0 and  = 0 (i.e., a symmetric geometric stable distribution or Linnik distribution with
= 0 (i.e., a symmetric geometric stable distribution or Linnik distribution with  =2), the distribution becomes the symmetric Laplace distribution with mean of 0, which has a probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
=2), the distribution becomes the symmetric Laplace distribution with mean of 0, which has a probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of:
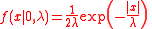
The Laplace distribution has a varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
equal to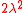 . However, for
. However, for  the variance of the geometric stable distribution is infinite.
the variance of the geometric stable distribution is infinite.
Relationship to the stable distribution
The stable distribution has the property that if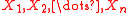 are independent, identically distributed random variables taken from a stable distribution, the sum
are independent, identically distributed random variables taken from a stable distribution, the sum 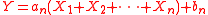 has the same distribution as the
has the same distribution as the 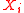 s for some
s for some 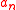 and
and 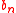 .
.
The geometric stable distribution has a similar property, but where the number of elements in the sum is a geometrically distributed random variable. If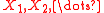 are independent and identically distributed random variablesIndependent and identically distributed random variablesIn probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
are independent and identically distributed random variablesIndependent and identically distributed random variablesIn probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
taken from a geometric stable distribution, the limitLimitA limit can be:* Limit :** Limit of a function** Limit of a sequence** One-sided limit** Limit superior and limit inferior** Limit of a net** Limit point** Limit ** Direct limit and Inverse limit...
of the sum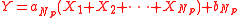 approaches the distribution of the
approaches the distribution of the 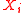 s for some coefficients
s for some coefficients  and
and  as p approaches 0, where
as p approaches 0, where 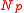 is a random variable independent of the
is a random variable independent of the 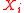 s taken from a geometric distribution with parameter p. In other words:
s taken from a geometric distribution with parameter p. In other words:
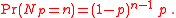
The distribution is strictly geometric stable only if the sum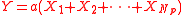 equals the distribution of the
equals the distribution of the 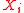 s for some a.
s for some a.
There is also a relationship between the stable distribution characteristic function and the geometric stable distribution characteristic function. The stable distribution has a characteristic function of the form:
-
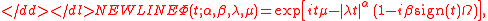
where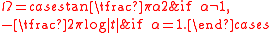
The geometric stable characteristic function can be expressed in terms of a stable characteristic function as:
-
-
-