
Geometry of numbers
Encyclopedia
In number theory
, the geometry of numbers studies convex bodies
and integer vectors in n-dimensional space. The geometry of numbers was initiated by .
The geometry of numbers has a close relationship with other fields of mathematics, especially functional analysis
and Diophantine approximation
, the problem of finding rational number
s that approximate an irrational quantity
.
Minkowski's theorem
, sometimes called Minkowski's first theorem, states that if

then K contains a nonzero vector in Γ.
The successive minimum λk is defined to be the inf
of the numbers λ such that λK contains k linearly independent vectors of Γ.
Minkowski's theorem on successive minima, sometimes called Minkowski's second theorem, is a strengthening of his first theorem and states that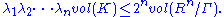
, Harold Davenport
and Carl Ludwig Siegel
). In recent years, Lenstra, Brion, and Barvinok have developed combinatorial theories that enumerate the lattice points in some convex bodies.
in 1972. It states that if L1,...,Ln are linearly independent
linear
forms in n variables with algebraic
coefficients and if ε>0 is any given real number, then
the non-zero integer points x with
lie in a finite number of proper subspaces
of Qn.
. Minkowski proved that symmetric convex bodies induce norms in finite-dimensional vector spaces. Minkwoski's theorem was generalized to topological vector space
s by Kolmogorov, whose theorem states that the symmetric convex sets that are closed and bounded generate the topology of a Banach space
.
Researchers continue to study generalizations to star-shaped sets and other non-convex set
s.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the geometry of numbers studies convex bodies
Convex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
and integer vectors in n-dimensional space. The geometry of numbers was initiated by .
The geometry of numbers has a close relationship with other fields of mathematics, especially functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
, the problem of finding rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s that approximate an irrational quantity
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
.
Minkowski's results
Suppose that Γ is a lattice in n-dimensional Euclidean space Rn and K is a convex centrally symmetric body.Minkowski's theorem
Minkowski's theorem
In mathematics, Minkowski's theorem is the statement that any convex set in Rn which is symmetric with respect to the origin and with volume greater than 2n d contains a non-zero lattice point...
, sometimes called Minkowski's first theorem, states that if

then K contains a nonzero vector in Γ.
The successive minimum λk is defined to be the inf
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the numbers λ such that λK contains k linearly independent vectors of Γ.
Minkowski's theorem on successive minima, sometimes called Minkowski's second theorem, is a strengthening of his first theorem and states that
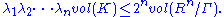
Later research in the geometry of numbers
In 1930-1960 research on the geometry of numbers was conducted by many number theorists (including Louis MordellLouis Mordell
Louis Joel Mordell was a British mathematician, known for pioneering research in number theory. He was born in Philadelphia, USA, in a Jewish family of Lithuanian extraction...
, Harold Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
and Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
). In recent years, Lenstra, Brion, and Barvinok have developed combinatorial theories that enumerate the lattice points in some convex bodies.
Subspace theorem of W. M. Schmidt
In the geometry of numbers, the subspace theorem was obtained by Wolfgang M. SchmidtWolfgang M. Schmidt
Wolfgang M. Schmidt is a mathematician born in 1933. He studied mathematics at the University of Vienna, where he received his PhD, which was supervised by Edmund Hlawka, in 1955...
in 1972. It states that if L1,...,Ln are linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
forms in n variables with algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
coefficients and if ε>0 is any given real number, then
the non-zero integer points x with

lie in a finite number of proper subspaces
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of Qn.
Influence on functional analysis
Minkowski's geometry of numbers had a profound influence on functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. Minkowski proved that symmetric convex bodies induce norms in finite-dimensional vector spaces. Minkwoski's theorem was generalized to topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s by Kolmogorov, whose theorem states that the symmetric convex sets that are closed and bounded generate the topology of a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
Researchers continue to study generalizations to star-shaped sets and other non-convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s.

