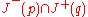Globally hyperbolic
Encyclopedia
In mathematical physics
, a spacetime
manifold
is globally hyperbolic if it satisfies a condition related to its causal structure
. This is relevant to Einstein's theory of general relativity
, and potentially to other metric gravitational theories.
To be precise, a spacetime manifold M without boundary is said to be globally hyperbolic if the following two conditions hold
A spacetime manifold with non-empty boundary is said to be globally hyperbolic if its interior, as a manifold in its own right, is globally hyperbolic.
Global hyperbolicity is completely equivalent to the existence of Cauchy surface
. In fact, this implies that a globally hyperbolic spacetime M is foliated by a family of Cauchy surfaces, i.e. the interior of M is topologically isomorphic (diffeomorphic
) to the product of the interior of some Cauchy surface Σ and some interval
I; the metric structure need not respect this decomposition, however. If the spatial boundary of M is non-empty and the metric non-singular there, it will be the boundary of all Cauchy surfaces of the family above. This essentially looks like a ring used to make soap bubbles with a lot of soap layers.
Summarized, a globally hyperbolic spacetime is a spacetime on which everything is determined by the equations of motion for one hypersurface, together with initial data specified on it. (At least if only fields are present which have a well-defined initial value formulation.) This is also the origin for the name of this property.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, a spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is globally hyperbolic if it satisfies a condition related to its causal structure
Causal structure
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.- Introduction :In modern physics spacetime is represented by a Lorentzian manifold...
. This is relevant to Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, and potentially to other metric gravitational theories.
To be precise, a spacetime manifold M without boundary is said to be globally hyperbolic if the following two conditions hold
- For every pair of points p and q in M, the space of all points that can be both reached from p along a past-oriented causal curve and reached from q along a future-oriented causal curve is compact. Note: We denote this compact space
-
- "Causality" holds on M (no closed timelike curveClosed timelike curveIn mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
s exist). Classically, a more restrictive and technical assumption is required, named strong causality (no "almost closed" timelike curves exist); but a recent result shows that causality suffices.
A spacetime manifold with non-empty boundary is said to be globally hyperbolic if its interior, as a manifold in its own right, is globally hyperbolic.
Global hyperbolicity is completely equivalent to the existence of Cauchy surface
Cauchy surface
Intuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
. In fact, this implies that a globally hyperbolic spacetime M is foliated by a family of Cauchy surfaces, i.e. the interior of M is topologically isomorphic (diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
) to the product of the interior of some Cauchy surface Σ and some interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
I; the metric structure need not respect this decomposition, however. If the spatial boundary of M is non-empty and the metric non-singular there, it will be the boundary of all Cauchy surfaces of the family above. This essentially looks like a ring used to make soap bubbles with a lot of soap layers.
Summarized, a globally hyperbolic spacetime is a spacetime on which everything is determined by the equations of motion for one hypersurface, together with initial data specified on it. (At least if only fields are present which have a well-defined initial value formulation.) This is also the origin for the name of this property.