
Causal structure
Encyclopedia
In mathematical physics
, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.
) spacetime
is represented by a Lorentzian manifold. The causal relations between points in the manifold are interpreted as describing which events in spacetime can influence which other events.
Minkowski spacetime is a simple example of a Lorentzian manifold. The causal relationships between points in Minkowski spacetime take a particularly simple form since the space is flat
. See Causal structure of Minkowski spacetime for more information.
The causal structure of an arbitrary (possibly curved) Lorentzian manifold is made more complicated by the presence of curvature
. Discussions of the causal structure for such manifolds must be phrased in terms of smooth
curve
s joining pairs of points. Conditions on the tangent vectors of the curves then define the causal relationships.
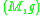 is a Lorentzian manifold (for metric
is a Lorentzian manifold (for metric
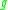 on manifold
on manifold
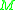 ) then the tangent vectors at each point in the manifold can be classed into three different types.
) then the tangent vectors at each point in the manifold can be classed into three different types.
A tangent vector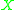 is
is
(Here we use the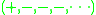 metric signature
metric signature
). A tangent vector is called "non-spacelike" if it is null or timelike.
These names come from the simpler case of Minkowski spacetime (see Causal structure of Minkowski spacetime).
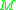 the timelike tangent vectors in the point's tangent space
the timelike tangent vectors in the point's tangent space
can be divided into two classes. To do this we first define an equivalence relation
on pairs of timelike tangent vectors.
If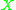 and
and 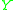 are two timelike tangent vectors at a point we say that
are two timelike tangent vectors at a point we say that 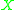 and
and 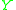 are equivalent (written
are equivalent (written 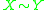 ) if
) if 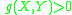 .
.
There are then two equivalence classes which between them contain all timelike tangent vectors at the point.
We can (arbitrarily) call one of these equivalence classes "future-directed" and call the other "past-directed". Physically this designation of the two classes of future- and past-directed timelike vectors corresponds to a choice of an arrow of time
at the point. The future- and past-directed designations can be extended to null vectors at a point by continuity.
A Lorentzian manifold is time-orientable if a continuous designation of future-directed and past-directed for non-spacelike vectors can be made over the entire manifold.
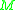 is a continuous map
is a continuous map 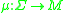 where
where 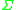 is a nondegenerate interval (i.e., a connected set containing more than one point) in
is a nondegenerate interval (i.e., a connected set containing more than one point) in 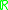 . A smooth path has
. A smooth path has 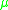 differentiable an appropriate number of times (typically
differentiable an appropriate number of times (typically 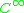 ), and a regular path has nonvanishing derivative.
), and a regular path has nonvanishing derivative.
A curve in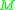 is the image of a path or, more properly, an equivalence class of path-images related by re-parametrisation, i.e. homeomorphism
is the image of a path or, more properly, an equivalence class of path-images related by re-parametrisation, i.e. homeomorphism
s or diffeomorphism
s of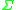 . When
. When 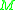 is time-orientable, the curve is oriented if the parameter change is required to be monotonic
is time-orientable, the curve is oriented if the parameter change is required to be monotonic
.
Smooth regular curves (or paths) in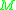 can be classified depending on their tangent vectors. Such a curve is
can be classified depending on their tangent vectors. Such a curve is
The requirements of regularity and nondegeneracy of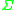 ensure that closed causal curves (such as those consisting of a single point) are not automatically admitted by all spacetimes.
ensure that closed causal curves (such as those consisting of a single point) are not automatically admitted by all spacetimes.
If the manifold is time-orientable then the non-spacelike curves can further be classified depending on their orientation with respect to time.
A chronological, null or causal curve in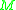 is
is
These definitions only apply to chronological, null and causal curves because only timelike or null tangent vectors can be assigned an orientation with respect to time.
between points and
and 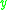 in the manifold
in the manifold 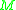 .
.
These relations are transitive
:
and satisfy
 in the manifold
in the manifold 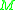 we define
we define
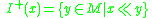
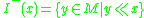
We similarly define
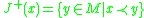
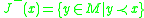
Points contained in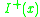 , for example, can be reached from
, for example, can be reached from  by a future-directed timelike curve.
by a future-directed timelike curve.
The point can be reached, for example, from points contained in
can be reached, for example, from points contained in 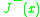 by a future-directed non-spacelike curve.
by a future-directed non-spacelike curve.
As a simple example, in Minkowski spacetime the set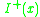 is the interior
is the interior
of the future light cone
at . The set
. The set 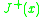 is the full future light cone at
is the full future light cone at  , including the cone itself.
, including the cone itself.
These sets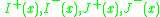
defined for all in
in 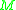 , are collectively called the causal structure of
, are collectively called the causal structure of 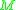 .
.
For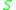 a subset
a subset
of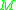 we define
we define
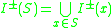
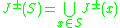
For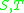 two subset
two subset
s of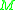 we define
we define
Topological
properties:
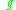 and
and 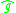 are conformally related if
are conformally related if 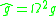 for some real function
for some real function 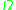 called the conformal factor. (See conformal map).
called the conformal factor. (See conformal map).
Looking at the definitions of which tangent vectors are timelike, null and spacelike we see they remain unchanged if we use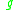 or
or 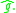 As an example suppose
As an example suppose 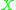 is a timelike tangent vector with respect to the
is a timelike tangent vector with respect to the 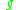 metric. This means that
metric. This means that 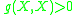 . We then have that
. We then have that 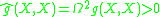 so
so 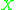 is a timelike tangent vector with respect to the
is a timelike tangent vector with respect to the 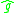 too.
too.
It follows from this that the causal structure of a Lorentzian manifold is unaffected by a conformal transformation.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.
Introduction
In modern physics (especially general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
) spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is represented by a Lorentzian manifold. The causal relations between points in the manifold are interpreted as describing which events in spacetime can influence which other events.
Minkowski spacetime is a simple example of a Lorentzian manifold. The causal relationships between points in Minkowski spacetime take a particularly simple form since the space is flat
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. See Causal structure of Minkowski spacetime for more information.
The causal structure of an arbitrary (possibly curved) Lorentzian manifold is made more complicated by the presence of curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. Discussions of the causal structure for such manifolds must be phrased in terms of smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s joining pairs of points. Conditions on the tangent vectors of the curves then define the causal relationships.
Tangent vectors
If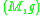 is a Lorentzian manifold (for metric
is a Lorentzian manifold (for metricMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
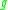 on manifold
on manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
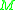 ) then the tangent vectors at each point in the manifold can be classed into three different types.
) then the tangent vectors at each point in the manifold can be classed into three different types.A tangent vector
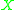 is
is
- timelike if
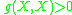
- null if
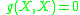
- spacelike if
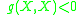
(Here we use the
 metric signature
metric signatureMetric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
). A tangent vector is called "non-spacelike" if it is null or timelike.
These names come from the simpler case of Minkowski spacetime (see Causal structure of Minkowski spacetime).
Time-orientability
At each point in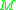 the timelike tangent vectors in the point's tangent space
the timelike tangent vectors in the point's tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
can be divided into two classes. To do this we first define an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on pairs of timelike tangent vectors.
If
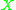 and
and 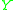 are two timelike tangent vectors at a point we say that
are two timelike tangent vectors at a point we say that 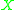 and
and 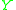 are equivalent (written
are equivalent (written 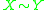 ) if
) if 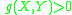 .
.There are then two equivalence classes which between them contain all timelike tangent vectors at the point.
We can (arbitrarily) call one of these equivalence classes "future-directed" and call the other "past-directed". Physically this designation of the two classes of future- and past-directed timelike vectors corresponds to a choice of an arrow of time
Arrow of time
The arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
at the point. The future- and past-directed designations can be extended to null vectors at a point by continuity.
A Lorentzian manifold is time-orientable if a continuous designation of future-directed and past-directed for non-spacelike vectors can be made over the entire manifold.
Curves
A path in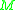 is a continuous map
is a continuous map 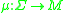 where
where 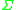 is a nondegenerate interval (i.e., a connected set containing more than one point) in
is a nondegenerate interval (i.e., a connected set containing more than one point) in 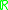 . A smooth path has
. A smooth path has 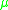 differentiable an appropriate number of times (typically
differentiable an appropriate number of times (typically 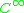 ), and a regular path has nonvanishing derivative.
), and a regular path has nonvanishing derivative.A curve in
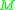 is the image of a path or, more properly, an equivalence class of path-images related by re-parametrisation, i.e. homeomorphism
is the image of a path or, more properly, an equivalence class of path-images related by re-parametrisation, i.e. homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s or diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s of
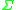 . When
. When 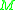 is time-orientable, the curve is oriented if the parameter change is required to be monotonic
is time-orientable, the curve is oriented if the parameter change is required to be monotonicMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
.
Smooth regular curves (or paths) in
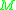 can be classified depending on their tangent vectors. Such a curve is
can be classified depending on their tangent vectors. Such a curve is
- chronological (or timelike) if the tangent vector is timelike at all points in the curve.
- null if the tangent vector is null at all points in the curve.
- spacelike if the tangent vector is spacelike at all points in the curve.
- causal (or non-spacelike) if the tangent vector is timelike or null at all points in the curve.
The requirements of regularity and nondegeneracy of
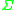 ensure that closed causal curves (such as those consisting of a single point) are not automatically admitted by all spacetimes.
ensure that closed causal curves (such as those consisting of a single point) are not automatically admitted by all spacetimes.If the manifold is time-orientable then the non-spacelike curves can further be classified depending on their orientation with respect to time.
A chronological, null or causal curve in
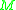 is
is
- future-directed if, for every point in the curve, the tangent vector is future-directed.
- past-directed if, for every point in the curve, the tangent vector is past-directed.
These definitions only apply to chronological, null and causal curves because only timelike or null tangent vectors can be assigned an orientation with respect to time.
- A closed timelike curve is a closed curve which is everywhere future-directed timelike (or everywhere past-directed timelike).
- A closed null curve is a closed curve which is everywhere future-directed null (or everywhere past-directed null).
- The holonomy of the ratio of the rate of change of the affine parameter around a closed null geodesic is the redshift factor.
Causal relations
There are two types of causal relationsRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
between points
 and
and 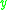 in the manifold
in the manifold 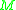 .
.-
 chronologically precedes
chronologically precedes 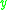 (often denoted
(often denoted 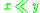 ) if there exists a future-directed chronological (timelike) curve from
) if there exists a future-directed chronological (timelike) curve from  to
to 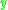 .
.
-
 causally precedes
causally precedes 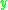 (often denoted
(often denoted 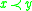 or
or 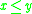 ) if there exists a future-directed causal (non-spacelike) curve from
) if there exists a future-directed causal (non-spacelike) curve from  to
to 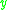 or
or  .
.
-
 strictly causally precedes
strictly causally precedes 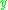 (often denoted
(often denoted 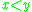 ) if there exists a future-directed causal (non-spacelike) curve from
) if there exists a future-directed causal (non-spacelike) curve from  to
to 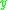 .
.
-
 horismos
horismos 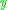 (often denoted
(often denoted 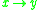 or
or 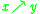 ) if
) if 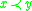 and
and 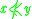 .
.
These relations are transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
:
-
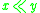 ,
, 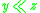 implies
implies 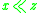
-
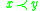 ,
, 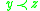 implies
implies 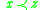
and satisfy
-
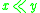 implies
implies 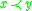 (this follows trivially from the definition)
(this follows trivially from the definition) -
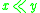 ,
, 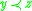 implies
implies 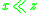
-
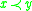 ,
, 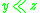 implies
implies 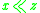
Causal structure
For a point in the manifold
in the manifold 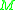 we define
we define
- The chronological future of
 , denoted
, denoted 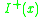 , as the set of all points
, as the set of all points 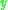 in
in 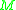 such that
such that  chronologically precedes
chronologically precedes 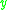 :
:
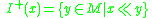
- The chronological past of
 , denoted
, denoted 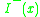 , as the set of all points
, as the set of all points 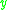 in
in 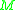 such that
such that 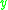 chronologically precedes
chronologically precedes  :
:
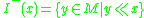
We similarly define
- The causal future (also called the absolute future) of
 , denoted
, denoted 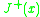 , as the set of all points
, as the set of all points 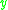 in
in 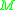 such that
such that  causally precedes
causally precedes 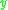 :
:
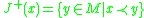
- The causal past (also called the absolute past) of
 , denoted
, denoted 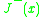 , as the set of all points
, as the set of all points 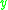 in
in 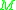 such that
such that 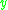 causally precedes
causally precedes  :
:
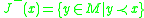
Points contained in
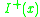 , for example, can be reached from
, for example, can be reached from  by a future-directed timelike curve.
by a future-directed timelike curve.The point
 can be reached, for example, from points contained in
can be reached, for example, from points contained in 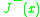 by a future-directed non-spacelike curve.
by a future-directed non-spacelike curve.As a simple example, in Minkowski spacetime the set
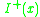 is the interior
is the interiorInterior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of the future light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
at
 . The set
. The set 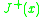 is the full future light cone at
is the full future light cone at  , including the cone itself.
, including the cone itself.These sets
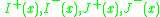
defined for all
 in
in 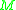 , are collectively called the causal structure of
, are collectively called the causal structure of 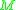 .
.For
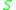 a subset
a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
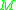 we define
we define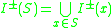
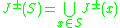
For
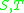 two subset
two subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of
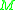 we define
we define- The chronological future of
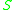 relative to
relative to 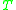 ,
, 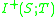 , is the chronological future of
, is the chronological future of 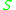 considered as a submanifold of
considered as a submanifold of 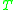 . Note that this is quite a different concept from
. Note that this is quite a different concept from 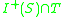 which gives the set of points in
which gives the set of points in 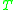 which can be reached by future-directed timelike curves starting from
which can be reached by future-directed timelike curves starting from 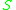 . In the first case the curves must lie in
. In the first case the curves must lie in 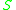 in the second case they do not. See Hawking and Ellis.
in the second case they do not. See Hawking and Ellis.
- The causal future of
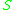 relative to
relative to 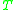 ,
, 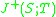 , is the causal future of
, is the causal future of 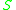 considered as a submanifold of
considered as a submanifold of 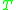 . Note that this is quite a different concept from
. Note that this is quite a different concept from 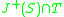 which gives the set of points in
which gives the set of points in 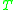 which can be reached by future-directed causal curves starting from
which can be reached by future-directed causal curves starting from 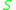 . In the first case the curves must lie in
. In the first case the curves must lie in 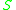 in the second case they do not. See Hawking and Ellis.
in the second case they do not. See Hawking and Ellis.
- A future set is a set closed under chronological future.
- A past set is a set closed under chronological past.
- An indecomposable past set is a past set which isn't the union of two different open past proper subsets.
-
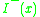 is a proper indecomposable past set (PIP).
is a proper indecomposable past set (PIP). - A terminal indecomposable past set (TIP) is an IP which isn't a PIP.
- The future Cauchy development of
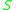 ,
, 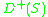 is the set of all points for which a past directed curve intersects
is the set of all points for which a past directed curve intersects 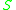 at least once. Similarly for the past Cauchy development. The Cauchy development is the union of the future and past Cauchy developments. Cauchy developments are important for the study of determinismDeterminismDeterminism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
at least once. Similarly for the past Cauchy development. The Cauchy development is the union of the future and past Cauchy developments. Cauchy developments are important for the study of determinismDeterminismDeterminism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
.
- A Cauchy surface is an acausal set whose Cauchy development is
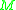 .
.
- A metric is globally hyperbolic if it can be foliated by Cauchy surfaces.
- The chronology violating set is the set of points through which closed timelike curves pass.
- The causality violating set is the set of points through which closed causal curves pass.
- For a causal curve
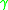 , the causal diamond is
, the causal diamond is 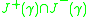 (here we are using the looser definition of 'curve' whereon it is just a set of points). In words: the causal diamond of a particle's world-line
(here we are using the looser definition of 'curve' whereon it is just a set of points). In words: the causal diamond of a particle's world-line 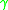 is the set of all events that lie in both the past of some point in
is the set of all events that lie in both the past of some point in 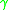 and the future of some point in
and the future of some point in 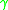 .
.
Properties
See Penrose, p13.- A point
 is in
is in 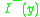 if and only if
if and only if 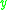 is in
is in 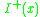 .
. -
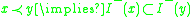
-
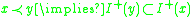
-
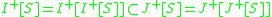
-
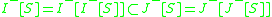
- The horismos is generated by null geodesic congruences.
Topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
properties:
-
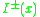 is open for all points
is open for all points  in
in 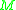 .
. -
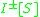 is open for all subsets
is open for all subsets 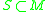 .
. -
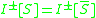 for all subsets
for all subsets 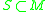 . Here
. Here 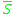 is the closureClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
is the closureClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
of a subset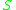 .
. -
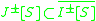
Conformal geometry
Two metrics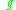 and
and 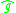 are conformally related if
are conformally related if 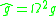 for some real function
for some real function 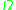 called the conformal factor. (See conformal map).
called the conformal factor. (See conformal map).Looking at the definitions of which tangent vectors are timelike, null and spacelike we see they remain unchanged if we use
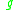 or
or 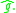 As an example suppose
As an example suppose 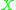 is a timelike tangent vector with respect to the
is a timelike tangent vector with respect to the 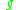 metric. This means that
metric. This means that 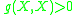 . We then have that
. We then have that 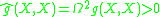 so
so 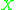 is a timelike tangent vector with respect to the
is a timelike tangent vector with respect to the 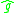 too.
too.It follows from this that the causal structure of a Lorentzian manifold is unaffected by a conformal transformation.
See also
- SpacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
- Lorentzian manifold
- Causality conditionsCausality conditionsIn the study of Lorentzian manifold spacetimes there exists a hierarchy of causality conditions which are important in proving mathematical theorems about the global structure of such manifolds. These conditions were collected during the late 1970s....
- Cauchy surfaceCauchy surfaceIntuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
- Globally hyperbolic manifold
- Closed timelike curveClosed timelike curveIn mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
- Penrose diagramPenrose diagramIn theoretical physics, a Penrose diagram is a two-dimensional diagram that captures the causal relations between different points in spacetime...
- Horismos
External links
- Turing Machine Causal Networks by Enrique Zeleny, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...

