Categories

• small provided that the class of all morphisms is a set (i.e., not a proper class); otherwise large.
• locally small provided that the morphisms between every pair of objects A and B form a set.
• Some authors assume a foundation in which the collection of all classes forms a "conglomerate", in which case a quasicategory is a category whose objects and morphisms merely form a conglomerate. (NB other authors use the term "quasicategory" with a different meaning.)
• isomorphic to a category B provided that there is an isomorphism between them.
• equivalent to a category B provided that there is an equivalence
  Equivalence of categories
  In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
  
   between them.
• concrete
  Concrete category
  In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
  
  provided that there is a faithful functor from A to Set
  Category of sets
  In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
  
  ; e.g., Vec
  Category of vector spaces
  In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
  
  , Grp
  Category of groups
  In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
  
  and Top
  Category of topological spaces
  In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
  
  .
• discrete
  Discrete category
  In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
  
  provided that each morphism is an identity morphism (of some object).
• thin category provided that there is at most one morphism between any pair of objects.
• a subcategory of a category B provided that there is an inclusion functor given from A to B.
• a full subcategory of a category B provided that the inclusion functor is full.
• wellpowered provided for each object A there is only a set of pairwise non-isomorphic subobject
  Subobject
  In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
  
  s.
• complete
  Complete category
  In mathematics, a complete category is a category in which all small limits exist. That is, a category C is complete if every diagram F : J → C where J is small has a limit in C. Dually, a cocomplete category is one in which all small colimits exist...
  
  provided that all small limits exist.
• cartesian closed
  Cartesian closed category
  In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
  
  provided that it has a terminal object and that any two objects have a product and exponential.
• abelian
  Abelian category
  In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
  
  provided that it has a zero object, it has all pullbacks and pushouts, and all monomorphisms and epimorphisms are normal.
• normal provided that every monic is normal.
• balanced if every bimorphism is an isomorphism.
• R-linear (R is a commutative ring
  Commutative ring
  In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
  
  ) if A is locally small, each hom set is an R-module, and composition of morphisms is R-bilinear. The category A is also said to be over R.

Morphisms

• an epimorphism
  Epimorphism
  In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
  
  provided that whenever . In other words, f is the dual of a monomorphism.
• an identity
  Identity (mathematics)
  In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
  
  provided that f maps an object A to A and for any morphisms g with domain A and h with codomain A,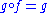 and .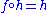
• an inverse
  Inverse (mathematics)
  In many contexts in mathematics the term inverse indicates the opposite of something. This word and its derivatives are used widely in mathematics, as illustrated below....
  
  to a morphism g if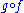 is defined and is equal to the identity morphism on the codomain of g, and 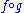is defined and equal to the identity morphism on the domain of g. The inverse of g is unique and is denoted by g⁻¹. f is a left inverse to g if is defined and is equal to the identity morphism on the domain of g, and similarly for a right inverse.
• an isomorphism
  Isomorphism
  In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations.  If there exists an isomorphism between two structures, the two structures are said to be isomorphic.  In a certain sense, isomorphic structures are...
  
  provided that there exists an inverse of f.
• a monomorphism
  Monomorphism
  In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
  
  (also called monic) provided that whenever ; e.g., an injection
  Injective function
  In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
  
   in Set
  Category of sets
  In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
  
  . In other words, f is the dual of an epimorphism.
• a retraction
  Section (category theory)
  In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
  
  if it has a right inverse.
• a coretraction
  Section (category theory)
  In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
  
  if it has a left inverse.

Functors

• a constant provided that F maps every object in a category to the same object A and every morphism to the identity on A.
• faithful provided that F is injective when restricted to each hom-set.
• full provided that F is surjective when restricted to each hom-set.
• isomorphism-dense (sometimes called essentially surjective) provided that for every B there exists A such that F(A) is isomorphic to B.
• an equivalence
  Equivalence of categories
  In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
  
  provided that F is faithful, full and isomorphism-dense.
• amnestic provided that if k is an isomorphism and F(k) is an identity, then k is an identity.
• reflect identities provided that if F(k) is an identity then k is an identity as well.
• reflect isomorphisms provided that if F(k) is an isomorphism then k is an isomorphism as well.

Objects

• isomorphic to an object B provided that there is an isomorphism between A and B.
• initial
  Initial object
  In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
  
  provided that there is exactly one morphism from A to each object B; e.g., empty set
  Empty set
  In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
  
   in Set
  Category of sets
  In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
  
  .
• terminal provided that there is exactly one morphism from each object B to A; e.g., singletons in Set
  Category of sets
  In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
  
  .
• a zero object if it is both initial and terminal, such as a trivial group
  Trivial group
  In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
  
   in Grp
  Category of groups
  In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
  
  .

• simple if it is not isomorphic to the zero object and any subobject
  Subobject
  In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
  
   of A is isomorphic to zero or to A.
• finite length if it has a composition series
  Composition series
  In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
  
  . The maximum number of proper subobjects in any such composition series is called the length of A.