
Gompertz-Makeham law of mortality
Encyclopedia
The Gompertz–Makeham law
states that the death rate is the sum of an age-independent component (the Makeham term, named after William Makeham) and an age-dependent component (the Gompertz function, named after Benjamin Gompertz
), which increases exponentially
with age. In a protected environment where external causes of death are rare (laboratory conditions, low mortality countries, etc.), the age-independent mortality component is often negligible. In this case the formula simplifies to a Gompertz law of mortality. In 1825, Benjamin Gompertz proposed an exponential increase in death rates with age.
The Gompertz–Makeham law of mortality describes the age dynamics of human mortality rather accurately in the age window from about 30 to 80 years of age. At more advanced ages, death rates do not increase as fast as predicted by this mortality law—a phenomenon known as the late-life mortality deceleration.
The decline in the human mortality rate
before the 1950s was mostly due to a decrease in the age-independent (Makeham) mortality component, while the age-dependent (Gompertz) mortality component was surprisingly stable. Since the 1950s, a new mortality trend has started in the form of an unexpected decline in mortality rates at advanced ages and "de-rectangularization" of the survival curve.
The hazard function which the Gompert-Makeham distribution is most often through characterised is
The quantile function
can be expressed in a closed-form expressions using the Lambert W function:
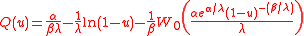
The Gompertz law is the same as a Fisher–Tippett distribution for the negative of age, restricted to negative values for the random variable
(positive values for age).
states that the death rate is the sum of an age-independent component (the Makeham term, named after William Makeham) and an age-dependent component (the Gompertz function, named after Benjamin Gompertz
Benjamin Gompertz
Benjamin Gompertz was a British self educated mathematician and actuary, who became a Fellow of the Royal Society...
), which increases exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
with age. In a protected environment where external causes of death are rare (laboratory conditions, low mortality countries, etc.), the age-independent mortality component is often negligible. In this case the formula simplifies to a Gompertz law of mortality. In 1825, Benjamin Gompertz proposed an exponential increase in death rates with age.
The Gompertz–Makeham law of mortality describes the age dynamics of human mortality rather accurately in the age window from about 30 to 80 years of age. At more advanced ages, death rates do not increase as fast as predicted by this mortality law—a phenomenon known as the late-life mortality deceleration.
The decline in the human mortality rate
Mortality rate
Mortality rate is a measure of the number of deaths in a population, scaled to the size of that population, per unit time...
before the 1950s was mostly due to a decrease in the age-independent (Makeham) mortality component, while the age-dependent (Gompertz) mortality component was surprisingly stable. Since the 1950s, a new mortality trend has started in the form of an unexpected decline in mortality rates at advanced ages and "de-rectangularization" of the survival curve.
The hazard function which the Gompert-Makeham distribution is most often through characterised is

The quantile function
Quantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
can be expressed in a closed-form expressions using the Lambert W function:
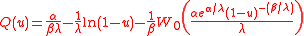
The Gompertz law is the same as a Fisher–Tippett distribution for the negative of age, restricted to negative values for the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
(positive values for age).
See also
- BiodemographyBiodemographyBiodemography is the science dealing with the integration of biology and demography.Biodemography is a new branch of human demography concerned with understanding the complementary biological and demographic determinants of and interactions between the birth and death processes that shape...
- Biodemography of human longevityBiodemography of human longevityBiodemography is a multidisciplinary approach, integrating biological knowledge with demographic research on human longevity and survival...
- GerontologyGerontologyGerontology is the study of the social, psychological and biological aspects of aging...
- DemographyDemographyDemography is the statistical study of human population. It can be a very general science that can be applied to any kind of dynamic human population, that is, one that changes over time or space...
- Life tableLife tableIn actuarial science, a life table is a table which shows, for each age, what the probability is that a person of that age will die before his or her next birthday...
- Maximum life spanMaximum life spanMaximum life span is a measure of the maximum amount of time one or more members of a population has been observed to survive between birth and death.Most living species have at least one upper limit on the number of times cells can divide...
- Reliability theory of aging and longevityReliability theory of aging and longevityReliability theory of aging and longevity is a scientific approach aimed to gain theoretical insights into mechanisms of biological aging and species survival patterns by applying a general theory of systems failure, known as reliability theory.-Overview:...

