Gravitational instanton
Encyclopedia
In mathematical physics
and differential geometry, a gravitational instanton is a four-dimensional complete Riemannian manifold
satisfying the vacuum
Einstein equations. They are so named because they are analogues in quantum theories of gravity
of instanton
s in Yang–Mills theory. In accordance with this analogy with self-dual Yang–Mills instantons, gravitational instantons are usually assumed to look like four dimensional Euclidean space
at large distances, and to have a self-dual Riemann tensor. Mathematically, this means that they are asymptotically locally Euclidean (or perhaps asymptotically locally flat) hyperkähler 4-manifolds
, and in this sense, they are special examples of Einstein manifold
s. From a physical point of view, a gravitational instanton is a non-singular solution of the vacuum Einstein equations with positive-definite, as opposed to Lorentzian
, metric.
There are many possible generalizations of the original conception of a gravitational instanton: for example one can allow gravitational instantons to have a nonzero cosmological constant
or a Riemann tensor which is not self-dual. One can also relax the boundary condition that the metric is asymptotically Euclidean.
There are many methods for constructing gravitational instantons, including the Gibbons–Hawking Ansatz, twistor theory
, and the hyperkähler quotient construction.
(viewed as the group Sp(1) or SU(2)). These can be defined in terms of Euler angles
by
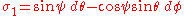
is important in many other contexts of geometry and theoretical physics. Its metric is given by
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
and differential geometry, a gravitational instanton is a four-dimensional complete Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
satisfying the vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
Einstein equations. They are so named because they are analogues in quantum theories of gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
of instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
s in Yang–Mills theory. In accordance with this analogy with self-dual Yang–Mills instantons, gravitational instantons are usually assumed to look like four dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
at large distances, and to have a self-dual Riemann tensor. Mathematically, this means that they are asymptotically locally Euclidean (or perhaps asymptotically locally flat) hyperkähler 4-manifolds
Hyperkähler manifold
In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...
, and in this sense, they are special examples of Einstein manifold
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
s. From a physical point of view, a gravitational instanton is a non-singular solution of the vacuum Einstein equations with positive-definite, as opposed to Lorentzian
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, metric.
There are many possible generalizations of the original conception of a gravitational instanton: for example one can allow gravitational instantons to have a nonzero cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
or a Riemann tensor which is not self-dual. One can also relax the boundary condition that the metric is asymptotically Euclidean.
There are many methods for constructing gravitational instantons, including the Gibbons–Hawking Ansatz, twistor theory
Twistor theory
In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
, and the hyperkähler quotient construction.
Properties
- A four-dimensional KählerKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
–Einstein manifoldEinstein manifoldIn differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
has a self-dual Riemann tensor. - Equivalently, a self-dual gravitational instanton is a four-dimensional complete hyperkähler manifoldHyperkähler manifoldIn differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...
. - Gravitational instantons are analogous to self-dual Yang–Mills instantonsInstantonAn instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
.
Taxonomy
By specifying the 'boundary conditions', i.e. the asymptotics of the metric 'at infinity' on a noncompact Riemannian manifold, gravitational instantons are divided into a few classes, such as asymptotically locally Euclidean spaces (ALE spaces), asymptotically locally flat spaces (ALF spaces). There also exist ALG spaces whose name is chosen by induction.Examples
It will be convenient to write the gravitational instanton solutions below using left-invariant 1-forms on the three-sphere S3(viewed as the group Sp(1) or SU(2)). These can be defined in terms of Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
by
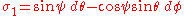
Taub–NUT metric
Eguchi–Hanson metric
The Eguchi–Hanson spaceEguchi–Hanson space
In mathematics and theoretical physics, the Eguchi–Hanson space is a non-compact, self-dual, asymptotically locally Euclidean metric on the cotangent bundle of the 2-sphere T*S2...
is important in many other contexts of geometry and theoretical physics. Its metric is given by
-
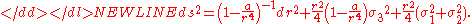
where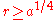
.
This metric is smooth everywhere if it has no conical singularity at
, 
. For 
this happens if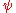 
has a period of 
, which gives a flat metric on R4; However for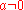 
this happens if 
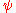has a period of 
.
Asymptotically (i.e., in the limit
) the metric looks like
which naively seems as the flat metric on R4. However, for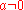
, 
has only half the usual periodicity, as we have seen. Thus the metric is asymptotically R4 with the identification 
, which is a Z2Cyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of SO(4)SO(4)In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO. The name comes from the fact that it is the special orthogonal group of order 4....
, the rotation group of R4. Therefore the metric is said to be asymptotically
R4/Z2.
There is a transformation to another coordinate systemCoordinate systemIn geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
, in which the metric looks like
where
).
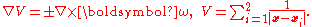In the new coordinates,
has the usual periodicity 
One may replace V by
For some n points
, i = 1, 2..., n.
This gives a multi-center Eguchi–Hanson gravitational instanton, which is again smooth everywhere if the angular coordinates have the usual periodicities (to avoid conical singularities). The asymptotic limit (
) is equivalent to taking all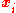 
to zero, and by changing coordinates back to r, 
and 
, and redefining 
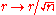, we get the asymptotic metric
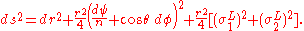
This is R4/Zn = C2/Zn, because it is R4 with the angular coordinate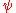
replaced by 
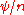, which has the wrong periodicity (
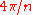instead of 
). In other words, it is R4 identified under 
, or, equivalnetly, C2 identified under zi ~ 
zi for i = 1, 2.
To conclude, the multi-center Eguchi–Hanson geometry is a KählerKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
Ricci flat geometry which is asymptotically C2/Zn. According to Yau's theorem this is the only geometry satisfying these properties. Therefore this is also the geometry of a C2/Zn orbifoldOrbifoldIn the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
in string theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
after its conical singularity has been smoothed away by its "blow up" (i.e., deformation) http://arxiv.org/abs/hep-th/9603167.
Gibbons–Hawking multi-centre metrics
where
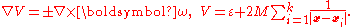
corresponds to multi-Taub–NUT, 
and 
is flat space, and 
and 
is the Eguchi–Hanson solution (in different coordinates).