
Green measure
Encyclopedia
In mathematics
— specifically, in stochastic analysis — the Green measure is a measure
associated to an Itō diffusion
. There is an associated Green formula representing suitably smooth function
s in terms of the Green measure and first exit times of the diffusion. The concepts are named after the British
mathematician
George Green
and are generalizations of the classical Green's function
and Green formula to the stochastic case using Dynkin's formula
.
of the form
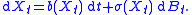
Let Px denote the law
of X given the initial condition X0 = x, and let Ex denote expectation
with respect to Px. Let LX be the infinitesimal generator
of X, i.e.
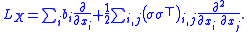
Let D ⊆ Rn be an open
, bounded
domain; let τD be the first exit time of X from D:
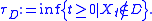
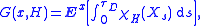
or for bounded, continuous functions f : D → R by
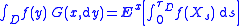
The name "Green measure" comes from the fact that if X is Brownian motion
, then
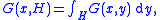
where G(x, y) is Green's function for the operator LX (which, in the case of Brownian motion, is ½Δ, where Δ is the Laplace operator
) on the domain D.
with compact support. Then
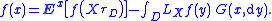
In particular, for C2 functions f with support compactly embedded
in D,
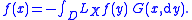
The proof of Green's formula is an easy application of Dynkin's formula and the definition of the Green measure:

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in stochastic analysis — the Green measure is a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
associated to an Itō diffusion
Ito diffusion
In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
. There is an associated Green formula representing suitably smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s in terms of the Green measure and first exit times of the diffusion. The concepts are named after the British
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
George Green
George Green
George Green was a British mathematical physicist who wrote An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism...
and are generalizations of the classical Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
and Green formula to the stochastic case using Dynkin's formula
Dynkin's formula
In mathematics — specifically, in stochastic analysis — Dynkin's formula is a theorem giving the expected value of any suitably smooth statistic of an Itō diffusion at a stopping time. It may be seen as a stochastic generalization of the fundamental theorem of calculus...
.
Notation
Let X be an Rn-valued Itō diffusion satisfying an Itō stochastic differential equationStochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
of the form
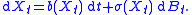
Let Px denote the law
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
of X given the initial condition X0 = x, and let Ex denote expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
with respect to Px. Let LX be the infinitesimal generator
Infinitesimal generator (stochastic processes)
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a stochastic process is a partial differential operator that encodes a great deal of information about the process...
of X, i.e.
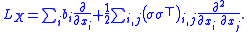
Let D ⊆ Rn be an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
domain; let τD be the first exit time of X from D:
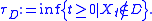
The Green measure
Intuitively, the Green measure of a Borel set H (with respect to a point x and domain D) is the expected length of time that X, having started at x, stays in H before it leaves the domain D. That is, the Green measure of X with respect to D at x, denoted G(x, ·), is defined for Borel sets H ⊆ Rn by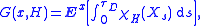
or for bounded, continuous functions f : D → R by
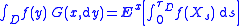
The name "Green measure" comes from the fact that if X is Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, then
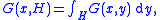
where G(x, y) is Green's function for the operator LX (which, in the case of Brownian motion, is ½Δ, where Δ is the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
) on the domain D.
The Green formula
Suppose that Ex[τD] < +∞ for all x ∈ D, and let f : Rn → R be of smoothness class C2Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
with compact support. Then
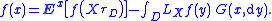
In particular, for C2 functions f with support compactly embedded
Compactly embedded
In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
in D,
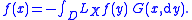
The proof of Green's formula is an easy application of Dynkin's formula and the definition of the Green measure:




