Gross-Neveu model
Encyclopedia
The Gross-Neveu model is a quantum field theory
model of Dirac fermion
s interacting via four fermion interactions in 1 spatial and 1 time dimension. It was introduced in 1974 by David Gross
and André Neveu
as a toy model
for quantum chromodynamics
, the theory of strong interactions.
It consists of N Dirac fermions, ψ1, ..., ψN. The Lagrangian density is
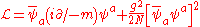
using the Einstein summation notation where g is the coupling constant
. If the mass m is nonzero, the model is massive classically, otherwise it enjoys a chiral symmetry
.
This model has an U(N)
global internal symmetry. When N=1 it reduces to the integrable Thirring model
.
It is a 2-dimensional version of the 4-dimensional Nambu–Jona-Lasinio model (NJL), which was introduced 14 years earlier as a model of quark confinement modeled upon the BCS theory
of superconductivity. The 2-dimensional version has the advantage that the 4-fermi interaction is renormalizable, which it is not in any higher number of dimensions.
. After demonstrating that this and related models are asymptotically free, they found that, in the subleading order, for small fermion masses the bifermion condensate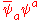
acquires a vacuum expectation value
(VEV) and as a result the fundamental fermions become massive. They find that the mass is not analytic in the coupling constant g. The vacuum expectation value spontaneously breaks
the chiral symmetry of the theory.
More precisely, expanding about the vacuum with no vacuum expectation value for the bilinear condensate they found a tachyon. To do this they solve the renormalization group equations
for the propagator
of the bifermion field, using the fact that the only renormalization of the coupling constant comes from the wave function renormalization
of the composite field. They then calculated, at leading order in a 1/N expansion but to all orders in the coupling constant, the dependence of the potential energy
on the condensate using the effective action
techniques introduced the previous year by Sidney Coleman
at the Erice
International Summer School of Physics. They found that this potential is minimized at a nonzero value of the condensate, indicating that this is the true value of the condensate. Expanding the theory about the new vacuum, the tachyon was found to be no longer present and in fact, like the BCS theory of superconductivity, there is a mass gap
.
They then made a number of general arguments about dynamical mass generation in quantum field theories. For example, they demonstrated that not all masses may be dynamically generated in theories which are infrared-stable, using this to argue that, at least to leading order in 1/N, the 4-dimensional
theory does not exist. They also argued that in asymptotically free theories the dynamically generated masses never depend analytically on the coupling constant
s.
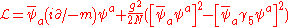
chosen so that the discrete chiral symmetry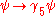
of the original model is enhanced to a continuous U(1)-valued chiral symmetry 
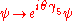. Chiral symmetry breaking
occurs as before, caused by the same VEV. However, as the spontaneously broken symmetry is now continuous, a massless Goldstone boson
appears in the spectrum. Although this leads to no problems at the leading order in the 1/N expansion, massless particles in 2-dimensional quantum field theories inevitably lead to infrared divergence
s and so the theory appears to not exist.
Two further modifications of the modified theory, which remedy this problem, were then considered. In one modification one increases the number of dimensions. As a result, the massless field does not lead to divergences. In the other modification, the chiral symmetry is gauged. As a result the Golstone boson is eaten by the Higgs mechanism
as the photon
becomes massive, and so does not lead to any divergences.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
model of Dirac fermion
Dirac fermion
In particle physics, a Dirac fermion is a fermion which is not its own anti-particle. It is named for Paul Dirac. All fermions in the standard model, except possibly neutrinos, are Dirac fermions...
s interacting via four fermion interactions in 1 spatial and 1 time dimension. It was introduced in 1974 by David Gross
David Gross
David Jonathan Gross is an American particle physicist and string theorist. Along with Frank Wilczek and David Politzer, he was awarded the 2004 Nobel Prize in Physics for their discovery of asymptotic freedom. He is currently the director and holder of the Frederick W...
and André Neveu
André Neveu
André Neveu is a French physicist working on string theory and quantum field theory who coinvented the Neveu-Schwarz algebra and the Gross-Neveu model.Neveu studied in Paris at the École normale supérieure...
as a toy model
Toy model
In physics, a toy model is a simplified set of objects and equations relating them that can nevertheless be used to understand a mechanism that is also useful in the full, non-simplified theory....
for quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, the theory of strong interactions.
It consists of N Dirac fermions, ψ1, ..., ψN. The Lagrangian density is
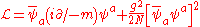
using the Einstein summation notation where g is the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
. If the mass m is nonzero, the model is massive classically, otherwise it enjoys a chiral symmetry
Chiral symmetry
In quantum field theory, chiral symmetry is a possible symmetry of the Lagrangian under which the left-handed and right-handed parts of Dirac fields transform independently...
.
This model has an U(N)
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
global internal symmetry. When N=1 it reduces to the integrable Thirring model
Thirring model
The Thirring model is an exactly solvable quantum field theory which describes the self-interactions of a Dirac field in two dimension.-Definition:The Thirring model is given by the Lagrangian density...
.
It is a 2-dimensional version of the 4-dimensional Nambu–Jona-Lasinio model (NJL), which was introduced 14 years earlier as a model of quark confinement modeled upon the BCS theory
BCS theory
BCS theory — proposed by Bardeen, Cooper, and Schrieffer in 1957 — is the first microscopic theory of superconductivity since its discovery in 1911. The theory describes superconductivity as a microscopic effect caused by a "condensation" of pairs of electrons into a boson-like state...
of superconductivity. The 2-dimensional version has the advantage that the 4-fermi interaction is renormalizable, which it is not in any higher number of dimensions.
Features of the theory
Gross and Neveu studied this model in the large N limit, expanding the relevant parameters in a 1/N expansion1/N expansion
In quantum field theory and statistical mechanics, the 1/N expansion is a particular perturbative analysis of quantum field theories with an internal symmetry group such as SO or SU...
. After demonstrating that this and related models are asymptotically free, they found that, in the subleading order, for small fermion masses the bifermion condensate
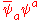acquires a vacuum expectation valueVacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
(VEV) and as a result the fundamental fermions become massive. They find that the mass is not analytic in the coupling constant g. The vacuum expectation value spontaneously breaks
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
the chiral symmetry of the theory.
More precisely, expanding about the vacuum with no vacuum expectation value for the bilinear condensate they found a tachyon. To do this they solve the renormalization group equations
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
for the propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
of the bifermion field, using the fact that the only renormalization of the coupling constant comes from the wave function renormalization
Wave function renormalization
In quantum field theory, wave function renormalization is a rescaling, or renormalization, of quantum fields to take into account the effects of interactions. For a noninteracting or free field, the field operator creates or annihilates a single particle with probability 1. Once interactions are...
of the composite field. They then calculated, at leading order in a 1/N expansion but to all orders in the coupling constant, the dependence of the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
on the condensate using the effective action
Effective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
techniques introduced the previous year by Sidney Coleman
Sidney Coleman
Sidney Richard Coleman was an American theoretical physicist who studied under Murray Gell-Mann.- Life and work :Sidney Coleman grew up on the Far North Side of Chicago...
at the Erice
Erice
Erice is a historic town and comune in the province of Trapani in Sicily, Italy.Erice is located on top of Mount Erice, at around 750m above sea level, overlooking the city of Trapani, the low western coast towards Marsala, the dramatic Punta del Saraceno and Capo san Vito to the north-east, and...
International Summer School of Physics. They found that this potential is minimized at a nonzero value of the condensate, indicating that this is the true value of the condensate. Expanding the theory about the new vacuum, the tachyon was found to be no longer present and in fact, like the BCS theory of superconductivity, there is a mass gap
Mass gap
In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest...
.
They then made a number of general arguments about dynamical mass generation in quantum field theories. For example, they demonstrated that not all masses may be dynamically generated in theories which are infrared-stable, using this to argue that, at least to leading order in 1/N, the 4-dimensional
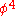theory does not exist. They also argued that in asymptotically free theories the dynamically generated masses never depend analytically on the coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
s.
Generalizations
Gross and Neveu considered several generalizations. First, they considered a Lagrangian with one extra quartic interaction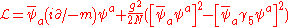chosen so that the discrete chiral symmetry
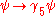of the original model is enhanced to a continuous U(1)-valued chiral symmetry 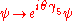. Chiral symmetry breakingChiral symmetry breaking
In particle physics, chiral symmetry breaking is an example of spontaneous symmetry breaking affecting the chiral symmetry of gauge theory such as Quantum Chromodynamics. The origin may be described as a fermion condensate...
occurs as before, caused by the same VEV. However, as the spontaneously broken symmetry is now continuous, a massless Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
appears in the spectrum. Although this leads to no problems at the leading order in the 1/N expansion, massless particles in 2-dimensional quantum field theories inevitably lead to infrared divergence
Infrared divergence
In physics, an infrared divergence or infrared catastrophe is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very small energy approaching zero, or, equivalently, because of physical phenomena at very long distances.The infrared ...
s and so the theory appears to not exist.
Two further modifications of the modified theory, which remedy this problem, were then considered. In one modification one increases the number of dimensions. As a result, the massless field does not lead to divergences. In the other modification, the chiral symmetry is gauged. As a result the Golstone boson is eaten by the Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
as the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
becomes massive, and so does not lead to any divergences.