Wave function renormalization
Encyclopedia
In quantum field theory
, wave function renormalization is a rescaling, or renormalization
, of quantum fields to take into account the effects of interactions. For a noninteracting or free field
, the field operator creates or annihilates a single particle with probability 1. Once interactions are included, however, this probability is modified in general to Z
1. This shows up when one calculates the propagator
beyond leading order; e.g., for a scalar field,
(The shift of the mass from m0 to m constitutes the mass renormalization.)
One possible wave function renormalization, which happens to be scale independent, is to rescale the fields so that the Lehmann weight (Z in the formula above) of their quanta is 1. (It's trickier to define it for unstable particles). For the purposes of studying renormalization group flows, if the coefficient of the kinetic term in the action at the scale Λ is Z, then the field is rescaled by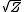
. A scale dependent wavefunction renormalization for a field means that that field has an anomalous scaling dimension
.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, wave function renormalization is a rescaling, or renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
, of quantum fields to take into account the effects of interactions. For a noninteracting or free field
Free field
In classical physics, a free field is a field whose equations of motion are given by linear partial differential equations. Such linear PDE's have a unique solution for a given initial condition....
, the field operator creates or annihilates a single particle with probability 1. Once interactions are included, however, this probability is modified in general to Z
1. This shows up when one calculates the propagatorPropagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
beyond leading order; e.g., for a scalar field,
(The shift of the mass from m0 to m constitutes the mass renormalization.)
One possible wave function renormalization, which happens to be scale independent, is to rescale the fields so that the Lehmann weight (Z in the formula above) of their quanta is 1. (It's trickier to define it for unstable particles). For the purposes of studying renormalization group flows, if the coefficient of the kinetic term in the action at the scale Λ is Z, then the field is rescaled by
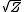. A scale dependent wavefunction renormalization for a field means that that field has an anomalous scaling dimensionAnomalous scaling dimension
In theoretical physics, by anomaly one usually means that the symmetry remains broken when the symmetry-breaking factor goes to zero.When the symmetry which is broken is scale invariance, then true power laws usually cannot be found from dimensional reasoning like in turbulence or quantum field...
.