
Gårding's inequality
Encyclopedia
In mathematics
, Gårding's inequality is a result that gives a lower bound for the bilinear form induced by a real linear elliptic partial differential operator
. The inequality is named after Lars Gårding
.
, open domain
in n-dimension
al Euclidean space
and let Hk(Ω) denote the Sobolev space
of k-times weakly differentiable functions u : Ω → R with weak derivatives in L2. Assume that Ω satisfies the k-extension property, i.e., that there exists a bounded linear operator E : Hk(Ω) → Hk(Rn) such that (Eu)|Ω = u for all u in Hk(Ω).
Let L be a linear partial differential operator of even order 2k, written in divergence form
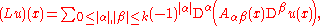
and suppose that L is uniformly elliptic, i.e., there exists a constant θ > 0 such that
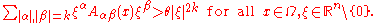
Finally, suppose that the coefficients Aαβ are bounded
, continuous function
s on the closure
of Ω for |α| = |β| = k and that

Then Gårding's inequality holds: there exist constants C and G ≥ 0
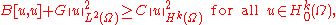
where
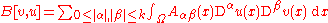
is the bilinear form associated to the operator L.
Δ. More specifically, suppose that one wishes to solve, for f ∈ L2(Ω) the Poisson equation
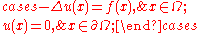
where Ω is a bounded Lipschitz domain
in Rn. The corresponding weak form of the problem is to find u in the Sobolev space H01(Ω) such that

where
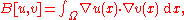
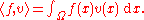
The Lax–Milgram lemma ensures that if the bilinear form B is both continuous and elliptic with respect to the norm on H01(Ω), then, for each f ∈ L2(Ω), a unique solution u must exist in H01(Ω). The hypotheses of Gårding's inequality are easy to verify for the Laplace operator Δ, so there exist constants C and G ≥ 0
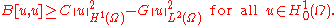
Applying the Poincaré inequality
allows the two terms on the right-hand side to be combined, yielding a new constant K > 0 with
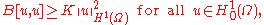
which is precisely the statement that B is elliptic. The continuity of B is even easier to see: simply apply the Cauchy-Schwarz inequality and the fact that the Sobolev norm is controlled by the L2 norm of the gradient.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Gårding's inequality is a result that gives a lower bound for the bilinear form induced by a real linear elliptic partial differential operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
. The inequality is named after Lars Gårding
Lars Gårding
Lars Gårding is a Swedish mathematician. He has made notable contributions to the study of partial differential operators. He is a professor emeritus of mathematics at Lund University in Sweden...
.
Statement of the inequality
Let Ω be a boundedBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, open domain
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and let Hk(Ω) denote the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
of k-times weakly differentiable functions u : Ω → R with weak derivatives in L2. Assume that Ω satisfies the k-extension property, i.e., that there exists a bounded linear operator E : Hk(Ω) → Hk(Rn) such that (Eu)|Ω = u for all u in Hk(Ω).
Let L be a linear partial differential operator of even order 2k, written in divergence form
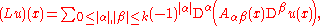
and suppose that L is uniformly elliptic, i.e., there exists a constant θ > 0 such that
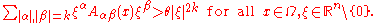
Finally, suppose that the coefficients Aαβ are bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
, continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of Ω for |α| = |β| = k and that

Then Gårding's inequality holds: there exist constants C and G ≥ 0
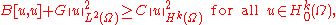
where
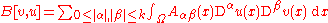
is the bilinear form associated to the operator L.
Application: the Laplace operator and the Poisson problem
As a simple example, consider the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
Δ. More specifically, suppose that one wishes to solve, for f ∈ L2(Ω) the Poisson equation
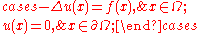
where Ω is a bounded Lipschitz domain
Lipschitz domain
In mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
in Rn. The corresponding weak form of the problem is to find u in the Sobolev space H01(Ω) such that

where
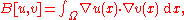
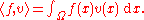
The Lax–Milgram lemma ensures that if the bilinear form B is both continuous and elliptic with respect to the norm on H01(Ω), then, for each f ∈ L2(Ω), a unique solution u must exist in H01(Ω). The hypotheses of Gårding's inequality are easy to verify for the Laplace operator Δ, so there exist constants C and G ≥ 0
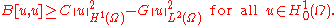
Applying the Poincaré inequality
Poincaré inequality
In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great...
allows the two terms on the right-hand side to be combined, yielding a new constant K > 0 with
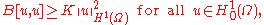
which is precisely the statement that B is elliptic. The continuity of B is even easier to see: simply apply the Cauchy-Schwarz inequality and the fact that the Sobolev norm is controlled by the L2 norm of the gradient.

