
Haagerup property
Encyclopedia
In mathematics
, the Haagerup property, also known as Gromov's a-T-menability, is a property of group
s that is a strong negation of Kazhdan
's property (T). Property (T) is considered a representation-theoretic form of rigidity, so the Haagerup property may be considered a form of strong nonrigidity; see below for details.
The Haagerup property is interesting to many fields of mathematics, including harmonic analysis
, representation theory
, operator K-theory
, and geometric group theory
.
Perhaps its most impressive consequence is that groups with the Haagerup Property satisfy the Baum-Connes conjecture and the related Novikov conjecture
. Groups with the Haagerup property are also uniformly embeddable
into a Hilbert space
.
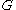 be a second countable locally compact group. The following properties are all equivalent, and any of them may be taken to be definitions of the Haagerup property:
be a second countable locally compact group. The following properties are all equivalent, and any of them may be taken to be definitions of the Haagerup property:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Haagerup property, also known as Gromov's a-T-menability, is a property of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s that is a strong negation of Kazhdan
Kazhdan
Kazhdan, also written as Kajdan, Kazdan, Každan, can mean:* Alexander Kazhdan - historian, byzantinist* David Kazhdan - mathematician.* Jerry Kazdan - mathematician...
's property (T). Property (T) is considered a representation-theoretic form of rigidity, so the Haagerup property may be considered a form of strong nonrigidity; see below for details.
The Haagerup property is interesting to many fields of mathematics, including harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, operator K-theory
Operator K-theory
In mathematics, operator K-theory is a variant of K-theory on the category of Banach algebras ....
, and geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
.
Perhaps its most impressive consequence is that groups with the Haagerup Property satisfy the Baum-Connes conjecture and the related Novikov conjecture
Novikov conjecture
The Novikov conjecture is one of the most important unsolved problems in topology. It is named for Sergei Novikov who originally posed the conjecture in 1965....
. Groups with the Haagerup property are also uniformly embeddable
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
into a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
.
Definitions
Let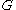 be a second countable locally compact group. The following properties are all equivalent, and any of them may be taken to be definitions of the Haagerup property:
be a second countable locally compact group. The following properties are all equivalent, and any of them may be taken to be definitions of the Haagerup property:- There is a proper continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
conditionally negative definite functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
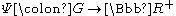 .
. 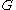 has the Haagerup approximation property, also known as Property
has the Haagerup approximation property, also known as Property 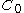 : there is a sequence of normalized continuous positive definite functions
: there is a sequence of normalized continuous positive definite functions  which vanish at infinity on
which vanish at infinity on 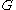 and converge to 1 uniformly on compact subsets of
and converge to 1 uniformly on compact subsets of 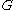 .
.- There is a strongly continuous unitary representationUnitary representationIn mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of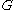 which weakly contains the trivial representationTrivial representationIn the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
which weakly contains the trivial representationTrivial representationIn the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
and whose matrix coefficients vanish at infinity on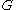 .
. - There is a proper continuous affine action of
 on a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
on a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
.
Examples
There are many examples of groups with the Haagerup property, most of which are geometric in origin. The list includes:- All compact groupCompact groupIn mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s (trivially). Note all compact groups also have property (T). The converse holds as well: if a group has both property (T) and the Haagerup property, then it is compact. - SO(n,1)
- SU(n,1)
- Groups acting properly on trees or on
 -trees
-trees - Coxeter groups
- Amenable groups
- Groups acting properly on CAT(0) cubical complexes

