Hahn embedding theorem
Encyclopedia
In mathematics
, especially in the area of abstract algebra
dealing with ordered structures on abelian group
s, the Hahn embedding theorem gives a simple description of all linearly ordered abelian group
s.
The theorem states: Any linearly ordered abelian group
can be embedded as an ordered subgroup of the additive group ℝΩ endowed with a lexicographical order
, where ℝ is the additive group of real numbers (with its standard order), and Ω is the set of Archimedean equivalence classes of
.
Let
denote the identity element of 
. For any nonzero 
∈
, exactly one of the elements 
or 
is greater than 
; denote this element by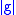 
. Two nonzero elements 
∈
are Archimedean equivalent if there exist natural numbers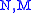 
∈ℕ such that 
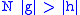and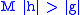 
. (Heuristically: neither 
nor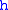 
is "infinitesimal" with respect to the other). The group 
is Archimedean
if all nonzero elements are Archimedean-equivalent. In this case, Ω is a singleton, so ℝΩ is just the group of real numbers. Then Hahn's Embedding Theorem reduces to Hölder
's theorem (which states that a linearly ordered abelian group is Archimedean
if and only if it is a subgroup of the ordered additive group of the real numbers).
gives a clear statement and proof of the theorem. The papers of and together provide another proof. See also .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
dealing with ordered structures on abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, the Hahn embedding theorem gives a simple description of all linearly ordered abelian group
Linearly ordered group
In abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
s.
The theorem states: Any linearly ordered abelian group
Linearly ordered group
In abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
can be embedded as an ordered subgroup of the additive group ℝΩ endowed with a lexicographical orderLexicographical order
In mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
, where ℝ is the additive group of real numbers (with its standard order), and Ω is the set of Archimedean equivalence classes of
.Let
denote the identity element of . For any nonzero ∈, exactly one of the elements or is greater than ; denote this element by 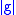. Two nonzero elements ∈ are Archimedean equivalent if there exist natural numbers 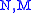∈ℕ such that 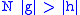and 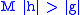. (Heuristically: neither nor 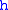is "infinitesimal" with respect to the other). The group is ArchimedeanArchimedean group
In abstract algebra, a branch of mathematics, an Archimedean group is an algebraic structure consisting of a set together with a binary operation and binary relation satisfying certain axioms detailed below. We can also say that an Archimedean group is a linearly ordered group for which the...
if all nonzero elements are Archimedean-equivalent. In this case, Ω is a singleton, so ℝΩ is just the group of real numbers. Then Hahn's Embedding Theorem reduces to Hölder
Otto Hölder
Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
's theorem (which states that a linearly ordered abelian group is Archimedean
Archimedean group
In abstract algebra, a branch of mathematics, an Archimedean group is an algebraic structure consisting of a set together with a binary operation and binary relation satisfying certain axioms detailed below. We can also say that an Archimedean group is a linearly ordered group for which the...
if and only if it is a subgroup of the ordered additive group of the real numbers).
gives a clear statement and proof of the theorem. The papers of and together provide another proof. See also .