
Hall-Janko graph
Encyclopedia
In the mathematical
field of graph theory
, the Hall–Janko graph, also known as the Hall-Janko-Wales graph, is a 36-regular
undirected graph with 100 vertices and 1800 edges.
It is a rank 3
strongly regular graph
with parameters (100,36,14,12) and a maximum coclique of size 10. This parameter set is not unique, it is however uniquely determined by its parameters as a rank 3 graph. The Hall–Janko graph was originally constructed by D. Wales to establish the existence of the Hall-Janko group as an index
2 subgroup of its automorphism group
.
The Hall–Janko graph can be constructed out of objects in U3(3), the simple group of order 6048:
The characteristic polynomial of the Hall–Janko graph is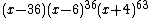 . Therefore the Hall–Janko graph is an integral graph
. Therefore the Hall–Janko graph is an integral graph
: its spectrum
consists entirely of integers.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Hall–Janko graph, also known as the Hall-Janko-Wales graph, is a 36-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
undirected graph with 100 vertices and 1800 edges.
It is a rank 3
Rank 3 permutation group
In mathematical finite group theory, a rank 3 permutation group is a group acting transitively on a set such that the stabilizer of a point has 3 orbits. The study of these groups was started by...
strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
with parameters (100,36,14,12) and a maximum coclique of size 10. This parameter set is not unique, it is however uniquely determined by its parameters as a rank 3 graph. The Hall–Janko graph was originally constructed by D. Wales to establish the existence of the Hall-Janko group as an index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 subgroup of its automorphism group
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
.
The Hall–Janko graph can be constructed out of objects in U3(3), the simple group of order 6048:
- In U3(3) there are 36 simple maximal subgroups of order 168. These are the vertices of a subgraph, the U3(3) graph. A 168-subgroup has 14 maximal subgroups of order 24, isomorphic to S4. Two 168-subgroups are called adjacent when they intersect in a 24-subgroup. The U3(3) graph is strongly regular, with parameters (36,14,4,6)
- There are 63 involutions (elements of order 2). A 168-subgroup contains 21 involutions, which are defined to be neighbors.
- Outside U3(3) let there be a 100th vertex C, whose neighbors are the 36 168-subgroups. A 168-subgroup then has 14 common neighbors with C and in all 1+14+21 neighbors.
- An involution is found in 12 of the 168-subgroups. C and an involution are non-adjacent, with 12 common neighbors.
- Two involutions are defined as adjacent when they generate a dihedral subgroup of order 8. An involution has 24 involutions as neighbors.
The characteristic polynomial of the Hall–Janko graph is
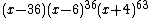 . Therefore the Hall–Janko graph is an integral graph
. Therefore the Hall–Janko graph is an integral graphIntegral graph
In the mathematical field of graph theory, an integral graph is a graph whose spectrum consists entirely of integers. In other words, a graphs is an integral graph if all the eigenvalues of its characteristic polynomial are integers....
: its spectrum
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
consists entirely of integers.

