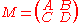Hamiltonian matrix
Encyclopedia
In mathematics
, a Hamiltonian matrix is any real matrix
that satisfies the condition that is symmetric, where is the skew-symmetric matrix
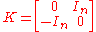
and is the identity matrix
.
In other words, is Hamiltonian if and only if
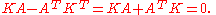
In the vector space
of all matrices,
Hamiltonian matrices form a subspace
of dimension .
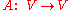 is called a Hamiltonian operator with respect to if the form
is called a Hamiltonian operator with respect to if the form  is symmetric. Equivalently, it
is symmetric. Equivalently, it
should satisfy
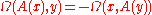
Choose a basis in , such that is written as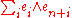 . A linear operator is Hamiltonian with respect to if and only if its matrix in this basis is Hamiltonian.
. A linear operator is Hamiltonian with respect to if and only if its matrix in this basis is Hamiltonian.
From this definition, the following properties are apparent.
A square of a Hamiltonian matrix is skew-Hamiltonian
. An exponential of a Hamiltonian matrix is symplectic, and a logarithm of a symplectic matrix is Hamiltonian.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Hamiltonian matrix is any real matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that satisfies the condition that is symmetric, where is the skew-symmetric matrix
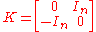
and is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
In other words, is Hamiltonian if and only if
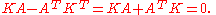
In the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of all matrices,
Hamiltonian matrices form a subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
of dimension .
Properties
- Let be a block matrixBlock matrixIn the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
given by
-
- where , , , and are matrices. Then is a Hamiltonian matrix provided that the matrices and are symmetric, and that .
- The transpose of a Hamiltonian matrix is Hamiltonian.
- The traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of a Hamiltonian matrix is zero. - The commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of two Hamiltonian matrices is Hamiltonian. - The eigenvalues of any Hamiltonian matrix are symmetric about the imaginary axis.
- The space of all Hamiltonian matrices is a Lie algebra
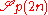 .
.
Hamiltonian operators
Let be a vector space, equipped with a symplectic form . A linear map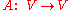 is called a Hamiltonian operator with respect to if the form
is called a Hamiltonian operator with respect to if the form  is symmetric. Equivalently, it
is symmetric. Equivalently, itshould satisfy
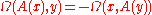
Choose a basis in , such that is written as
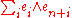 . A linear operator is Hamiltonian with respect to if and only if its matrix in this basis is Hamiltonian.
. A linear operator is Hamiltonian with respect to if and only if its matrix in this basis is Hamiltonian.From this definition, the following properties are apparent.
A square of a Hamiltonian matrix is skew-Hamiltonian
Skew-Hamiltonian matrix
In linear algebra, skew-Hamiltonian matrices are special matrices which correspond to skew-symmetric bilinear forms on a symplectic vector space.Let V be a vector space, equipped with a symplectic form \Omega. Such a space must be even-dimensional...
. An exponential of a Hamiltonian matrix is symplectic, and a logarithm of a symplectic matrix is Hamiltonian.