Skew-Hamiltonian matrix
Encyclopedia
In linear algebra
, skew-Hamiltonian matrices are special matrices
which correspond to skew-symmetric bilinear forms on a symplectic vector space
.
Let V be a vector space
, equipped with a symplectic form
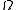. Such a space must be even-dimensional. A linear map 
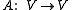is called a skew-Hamiltonian operator with respect to 
if the form 
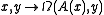is skew-symmetric.
Choose a basis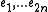
in V, such that 
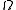is written as 
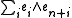. Then a linear operator is skew-Hamiltonian with respect to 
if and only if its matrix A satisfies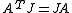 
, where J is the skew-symmetric matrix
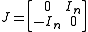
and In is the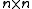
identity matrix
. Such matrices are called skew-Hamiltonian.
The square of a Hamiltonian matrix is skew-Hamiltonian. The converse is also true: every skew-Hamiltonian matrix can be obtained as the square of a Hamiltonian matrix.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, skew-Hamiltonian matrices are special matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which correspond to skew-symmetric bilinear forms on a symplectic vector space
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
.
Let V be a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, equipped with a symplectic form
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
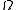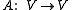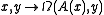. Such a space must be even-dimensional. A linear map is called a skew-Hamiltonian operator with respect to if the form is skew-symmetric.Choose a basis
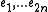in V, such that 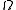is written as 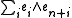. Then a linear operator is skew-Hamiltonian with respect to if and only if its matrix A satisfies 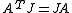, where J is the skew-symmetric matrix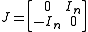and In is the
identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. Such matrices are called skew-Hamiltonian.
The square of a Hamiltonian matrix is skew-Hamiltonian. The converse is also true: every skew-Hamiltonian matrix can be obtained as the square of a Hamiltonian matrix.